概率图模型

概率图模型是一类用图来表示变量之间的关系的概率模型，把一个个变量看成图中的一个个节点，变量之间如果存在关系就用线连起来，根据线的有向和无向，可以进一步划分为有向图模型和无向图模型：
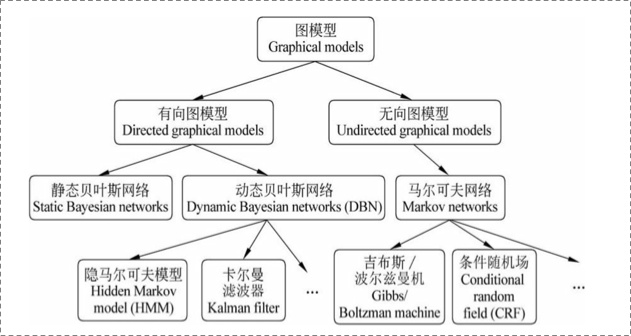
ポジショニングマップ
所谓有向无向就是指变量之间到底是单向的依赖还是互相依赖，具体来说，就是如何求一系列变量发生的联合概率P(x1,x2,...,xn)。

对于有向图来说，联合概率的求法是：
$$P(x_1, ..., x_n) = \prod_{i=0} P(x_i |\pi (x_i)) $$
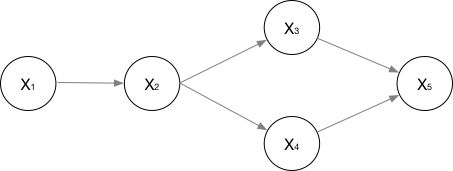
ポジショニングマップ
比如对于上图，就可以这样计算联合概率：
$$P(x_1, ..., x_5) = P(x_1)*P(x_2 |x_1)*P(x_3 |x_2)*P(x_4 |x_2)*P(x_5 |x_3,x_4) $$

对于无向图，在了解怎么求它的联合概率之前，先定义几个概念。

首先，因为无向图不像有向图那样定义了节点之间的拓扑顺序，所以无法用链式法则对p(x)逐一分解，无向图模型的联合概率一般通过全连通子图为单位进行分解，而无向图中的一个全连通子图就称为团：
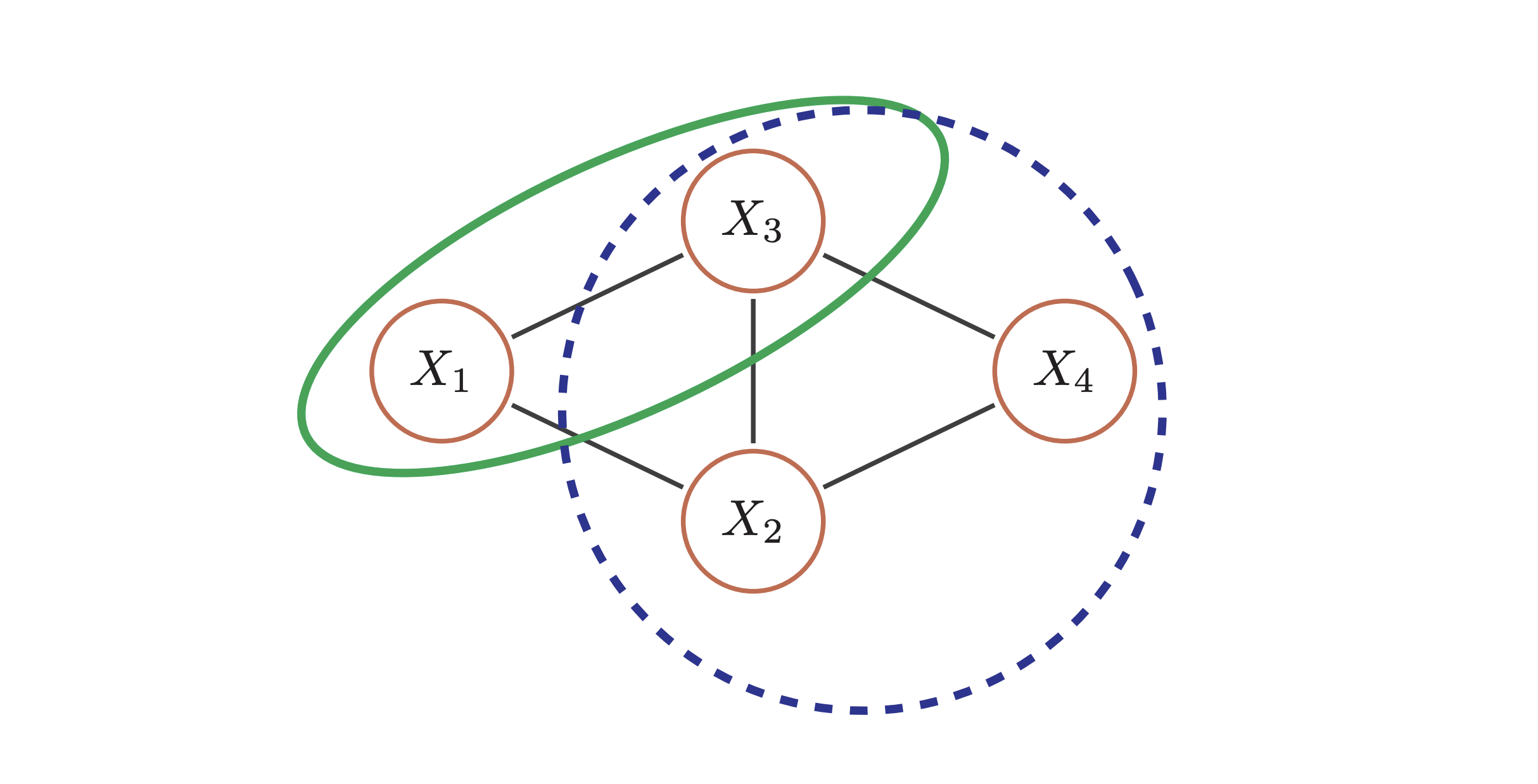
ポジショニングマップ
具体来说，全连通子团里的所有节点之间都是相连的，比如上图中的：{x1,x2}、{x1,x2,x3}等等

如果一个团不能被其他团包含，这个团就是一个最大团，比如图中蓝色那部分，为什么这是一个最大团，因为x1无法和它构成一个更大的团（在这里x1没有和x4相连）。

基于以上的概念，无向图的联合概率定义为一系列的最大团上的非负函数的乘积。

Hammersley-Clifford定理：如果一个分布p(x)>0满足无向图G中的局部马尔可夫性质，当且仅当p(x)可以表示为一系列定义在最大团上的非负函数的乘积形式，即
$$p(x) = \frac{1}{Z} \prod _{c \in C} \phi_c (x_c)$$
其中C为G中的是最大团集合，phi是定义在团c上的势能函数，Z是配分函数，用来将乘积归一化为概率形式：
$$Z = \sum_{x} \prod_{c \in C} \phi_c (x_c)$$
对于这个势能函数，针对不同的模型有不同的定义，这里暂不详细说明。

以上就是对概率图模型的简单介绍，简单来说，这是一种通过图结构来描述多元随机变量之间条件独立关系的概率模型，可以看到，其实它作了一个很重要的假设，独立性假设，认为k个随机变量可以分解为k个条件概率的乘积，大大减少了整个模型的参数，不然如果考虑所有情况，这样模型的参数量将十分巨大，计算机很难计算。