隐马尔可夫模型
之前介绍了概率图模型,而隐马尔可夫模型就属于其中的有向图模型。
首先来回顾一下马尔可夫假设:无记忆性,也就是这一时刻的状态只受前一时刻的影响,而不受再往前时刻的状态影响。
现在来举一个例子说明一下什么是隐马尔可夫模型:
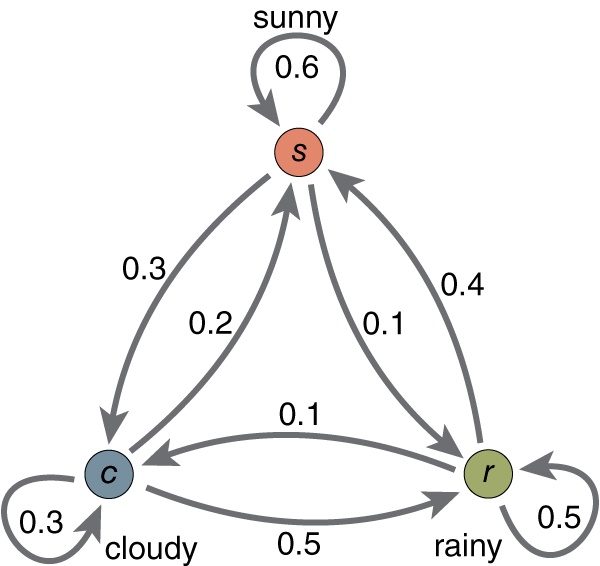
上面就是一个概率图模型,可以看出这是有向图,一共有三种状态:sunny、rainy、cloudy,同时上图也表明了状态之间的转移概率,这些状态是不可被观察的,也被称为隐变量。除此之外,还有一个可以被观察的观测变量,两者就共同构成一个隐马尔可夫模型:
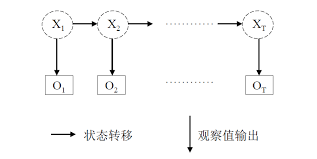
观察变量可以是某个人的活动,比如散步购物在家打扫,这些活动和天气,也就是状态变量之间存在着关系:
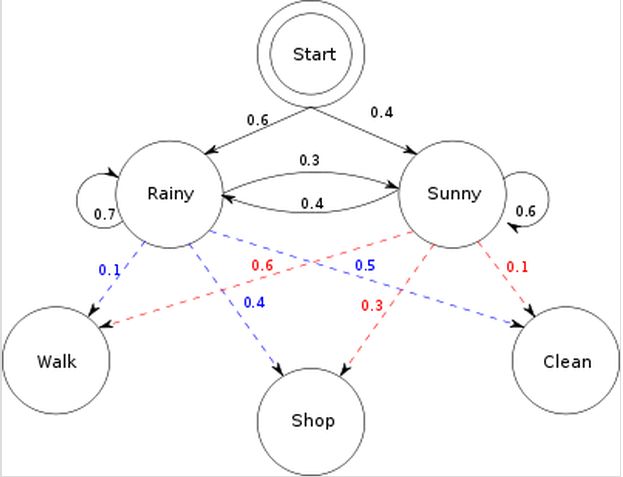
所以总的来说,一个隐马尔可夫模型包括三个要素,第一是状态转移概率,是模型在各个状态之间转换的概率,在这个例子就是指今天是晴天明天雨天这类概率。第二点是输出观测概率,是模型根据当前状态获得各个观测值的概率,在这个例子指在某种天气下某个人做某个活动的概率。第三点是初始状态概率,是模型在初始时刻各状态出现的概率。
基于上面的三个基本要素,我们就可以构建出一个隐马尔可夫模型,在实际应用中,我们往往会基于这个模型解决三类问题:
第一个是给定模型的状态转移概率、输出观测概率、初始状态概率,如何有效地计算产生观测序列的概率,或者说,如何评估模型和观测序列之间的匹配程度。
第二个是给定模型的状态转移概率、输出观测概率、初始状态概率和观测序列,如何找到与观测序列最匹配的状态序列,也就是从观测序列推断出隐藏的模型状态。
第三个是给定观测序列,如何调整模型的状态转移概率、输出观测概率、初始状态概率,使得观测序列出现的概率最大,也就是如何训练模型使得其能最好地描述观测数据。
针对这三个问题都有各自的算法解决,这里暂不详细介绍。