Jesse Yule's Blog

泊松回归

泊松回归是广义线性回归模型中的一种，除了泊松回归广义线性模型还有负二项、逻辑、gamma等等，之所以这里主要把泊松回归拿出来讲，是最近发现它的变型还挺多的，而且用得也比较多。

首先我们来谈谈泊松回归的定义，从GLM的角度来说，泊松回归就是针对服从泊松分布的响应变量进行回归分析。泊松分布描述的是某段时间内事件发生次数的概率，既然是次数就说明了响应变量是整数，也就是说，只要我们看到响应变量是整数，就可以考虑泊松分布建模（其实还有负二项分布），这就是泊松分布比较常用的原因。

$$P(X=k)=\frac{e^\lambda \lambda^k}{k!}$$

泊松分布有一个特点，那就是期望和方差都为lambda，换句话说，假如我们用泊松回归，就假设了随着数据量增大，数据的均值和方差会越来越接近。实际上，响应变量观察到的方差很可能比泊松分布预测的方差要大，这就导致了一种称为过度离势（over dispersion）的问题，同时也催生出泊松回归的第一种变型，over-dispersed poisson model，或者说类泊松分布。

这里暂不谈论太多过度离势的原因，就说一个很严重的后果，假如在存在过度离势我们仍然使用泊松回归，就无法对变量的p值进行正确的判断，比如下图是我用泊松回归（左）和类泊松回归（右）分析得到的结果：

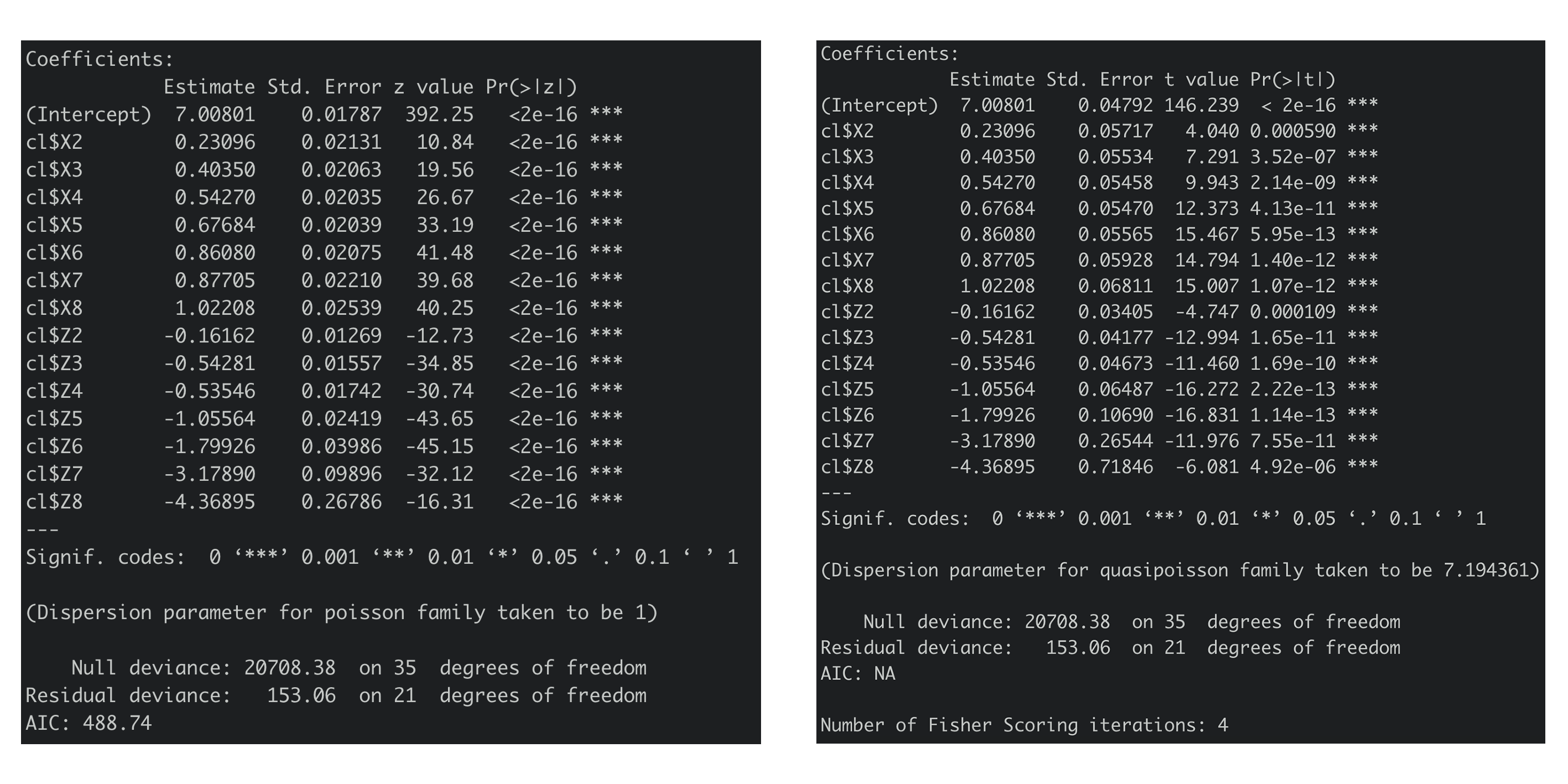
主要关注几点，第一，不论是泊松还是类泊松，参数估计的结果都是一样的，第二，类泊松的参数方差、p值等是改变的，这里或许还不够明显，但有时候p值会变得过大，这时候我们就不能在模型中继续使用这个变量了（详情可查看之前写的用GLM进行数据分析系列文章）。

在应用泊松分布，除了过度离势问题，还有一个值得注意的问题，就是0点有过多数值：

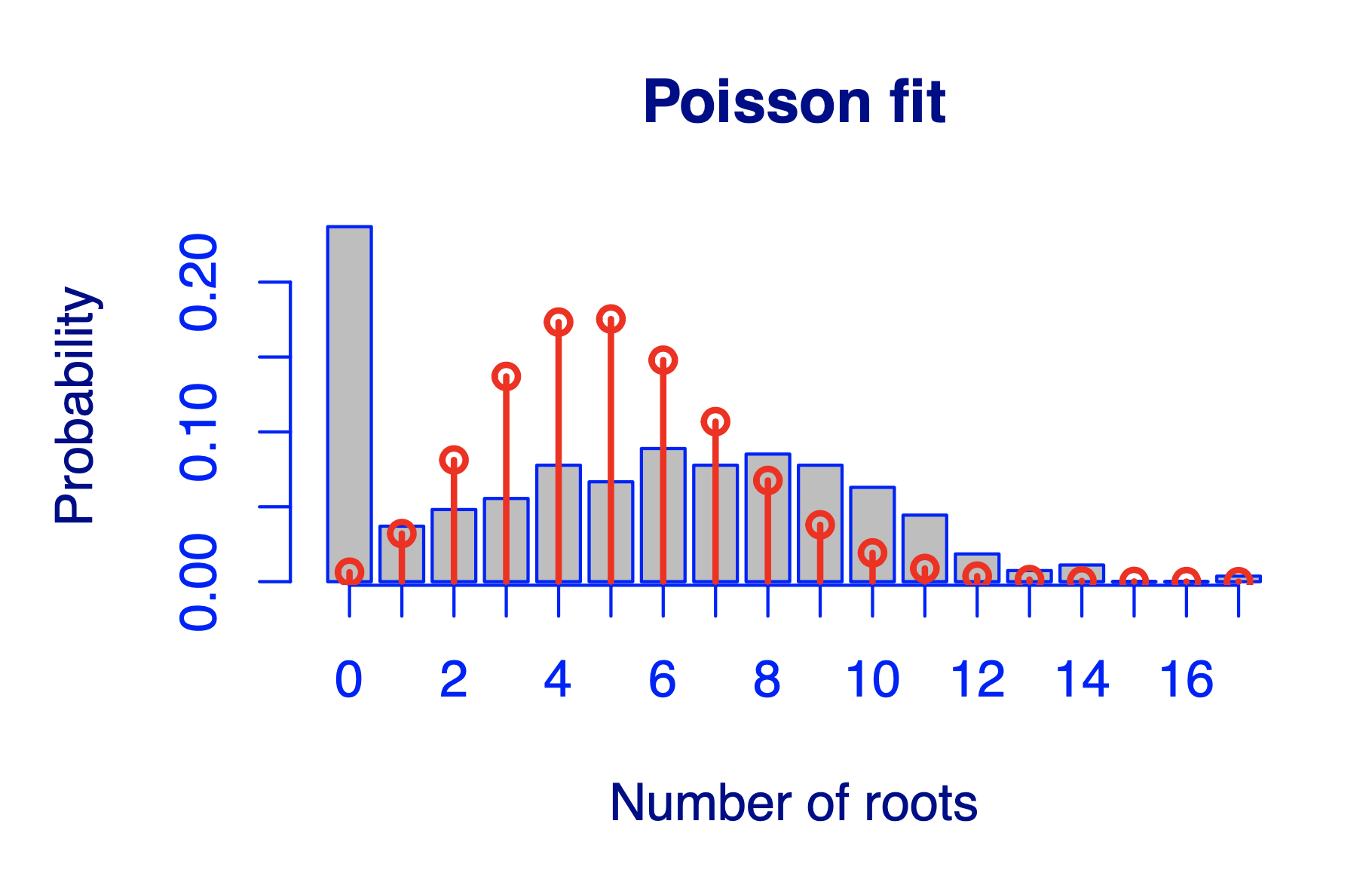
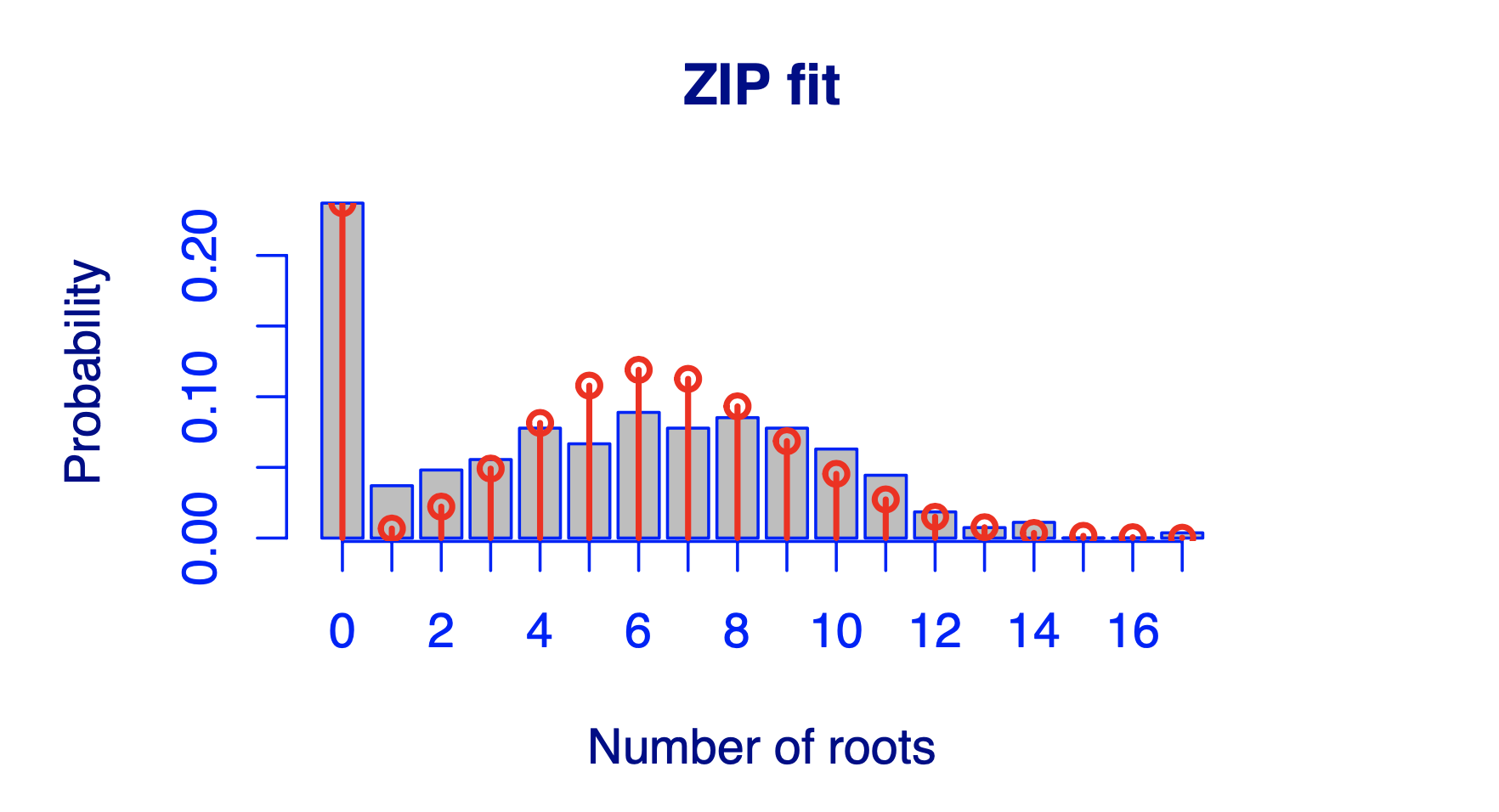
通过上图可以看出，大量数据的取值为0，只时候我们用了泊松回归得到的效果也一点都不好，所以就有了第二种变型，zero-inflated poisson distribution（中文翻译貌似是零膨胀泊松分布）。

所谓的零膨胀模型，其实就是针对那些在零点占很大比重的数据进行分析的模型。主要是假设零计数数据和服从泊松分布的计数数据各占一定比例，共同构成一个混合分布。以zip（zero-inflated poisson）为例：

$$P(Y_i = y_i) = \begin{cases} p + (1-p)f(0) & \text{y_i=0}\\ (1-p)f(y_i) & \text{y_i>0} \end{cases}$$

其中，f就是泊松分布：

$$f(y_i) =\frac{\lambda_i^{y_i}}{y_i !}exp(-\lambda_i)$$

式中p越大就说明数据中0的比例越大，当p=0，分布就变成正常的泊松分布。

现在我们已经知道了响应变量的分布，下一步要做的就是分析响应变量和解释变量之间的关系，这里直接给出答案，只要是通过分布中的p和lambda分别和解释变量构成联系的：

$$log \mu_i = \beta x_{i1}$$

$$log \frac{\pi_i}{1-\pi_i} = \gamma x_{i2}$$

其中，xi1和xi2都是取自解释变量的一部分或全部，可能相同也可能不同。整个建模过程，可以看成是首先估计出p和mu的取值，使得响应变量的分布能尽可能接近观测值，然后，再用解释变量去拟合这两个参数。

最后，用零膨胀泊松模型去重新分析一下，得到的结果就明显比之前好很多了。