蒙特卡罗方法
蒙特卡罗方法也叫统计模拟法、随机抽样技术,我觉得它不是只是一个方法,更是一种思想或者一类方法的统称。
蒙特卡罗方法的基本思路是:所求解问题是某随机事件A出现的概率,通过某些实验方法,得出A事件出现的频率,以此估计A事件出现的概率。
上面的描述可能还有点抽象,这里举一个著名的例子,求圆周率。

如果希望求圆周率可以先从求圆的面积开始,这里选择随机在正方形内部均匀生成样本点,统计落在圆内的点占所有点的比例,根据正方形的面积去推导圆的面积,再反推圆周率,其中求面积比例的过程就是基于频率估计概率的过程,也就是蒙特卡罗的核心思想。
接下来再介绍一下拒绝采样,其实之前也介绍过了,这里再重新分析一下。拒绝采样的目标就是根据概率密度函数f(x)生成样本X,如果这个f(x)比较复杂没办法通过电脑直接生成样本,我们就需要一个简单的可以直接生成样本的概率密度函数g(y)和均匀分布U去辅助它。
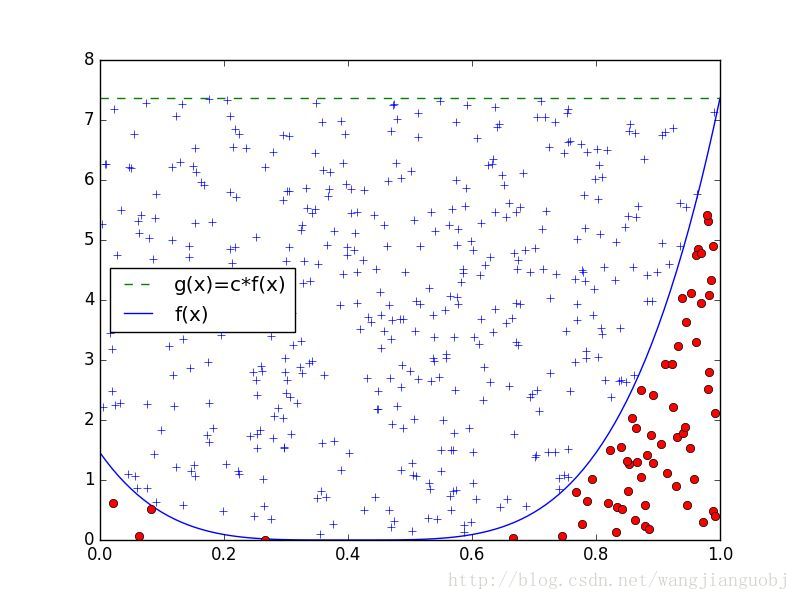
为了直观解释,我们选择了均匀分布作为g(x),首先我们确定一个常数c,使得c*g(x)能够覆盖f(x),每次我们生成两个样本Y和U,对应上图的矩阵内的一点(Y, U*c*g(Y)),如果U*c*g(Y)小于f(Y),即点在f(Y)下方,我们就接受这个样本,认为它服从f(x)的分布。
可以看到,上述的采样方法和求解圆周率的思想是异曲同工的,蒙特卡洛方法的精髓就在于这种大量随机采样,根据样本进一步进行分析。