从线性回归到广义线性模型
在谈及广义线性模型是什么之前,我想先分析一下线性回归模型有什么限制。在这里先说明一点,以下分析的线性回归模型,是考虑了随机误差项的完整的线性回归模型。
首先我想说明一下关于响应变量(y)的分布,以及响应变量和解释变量(x)之间的关系的区别。在线性回归中,往往我们会认为响应变量服从正态分布(且方差不变)、响应变量和解释变量之间服从线性关系,这时候我们使用线性回归才能得到好的效果,那么我们应该怎么理解这两者呢,首先来看一下图:
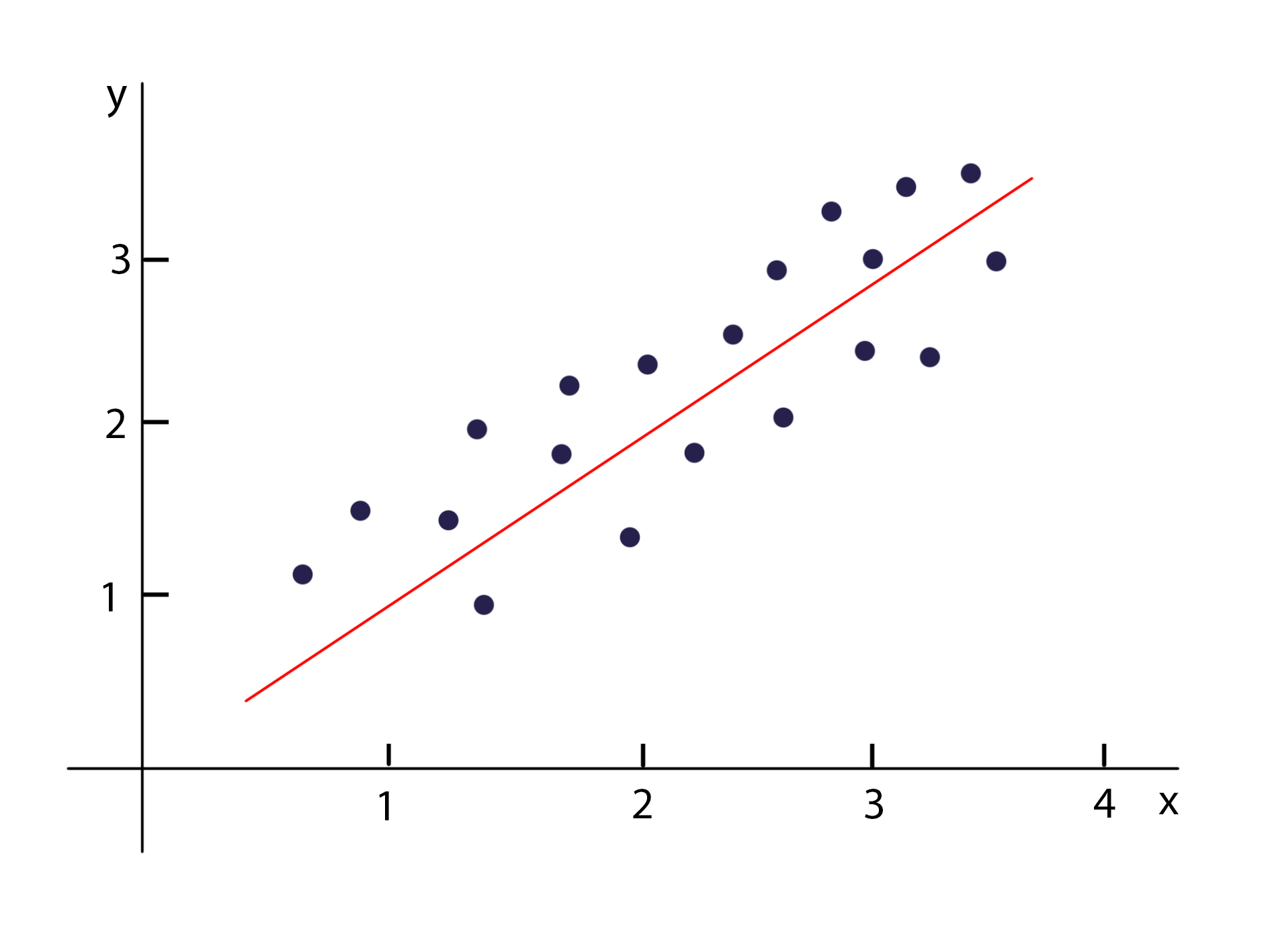
这是一个很经典的线性分布的数据,可以看到随着x增大y也增大,而且两个的关系能够用一条直线近似表达,所以我们说x和y之间有线性关系。如果我们只看y的数据,也就是说把这个二维图降维到只有y轴:

上图就相当于把最初的图的点投影到y轴上,这时候没有了x,反映的就是y的数据的分布状况。
明白了什么是响应变量的分布之后,就开始正式讨论线性回归的局限性。首先,正如一开始说的,线性回归的响应变量需要服从正态分布,这是基于高斯-马尔可夫定理得到的:在线性回归模型中,如果误差满足零均值、同方差且互不相关,则回归系数的最佳线性无偏估计就是普通最小二乘法估计。或者简单来说,这时候使用最小二乘法的线性回归的估计效果最好。
要说清楚这个结论,还是从头推导一次比较好。首先,我们还记得线性回归模型可以表达为:
a_0、a_1是非随机但不可观察的参数,X_i是非随机且可观察的一般变量,e_i是不可观察的随机变量,因此Yi是可观察的随机变量。对于一个把随机误差也考虑的完整的线性回归模型,模型的输出并不等于回归方程的输出,还需要加上随机误差项。响应变量因为考虑了随机误差而被看作随机变量。我们基于数据拟合一个线性回归模型,其实只是求出a_0、a_1这两个参数,主要是基于最小化损失函数(最小二乘法)得到的:
其中,Y_i'是真实数据(观察数据),因为模型考虑了随机误差,所以这里可以假设,观察数据等于我们训练完成后的线性回归模型的输出,所以,当我们最小化了损失函数,我们就可以得到:
以上的式子说明了,即使响应变量和解释变量确实服从线性关系,即使模型已经训练完成,因为随机误差的存在,损失函数也不可能等于0。在这里我们可以得到一个结论,对于一个训练完成的线性回归模型,它的损失函数和随机误差项是相关的。
接下来我们再看另一个例子,现在我们基于数据做线性回归得到一个模型:
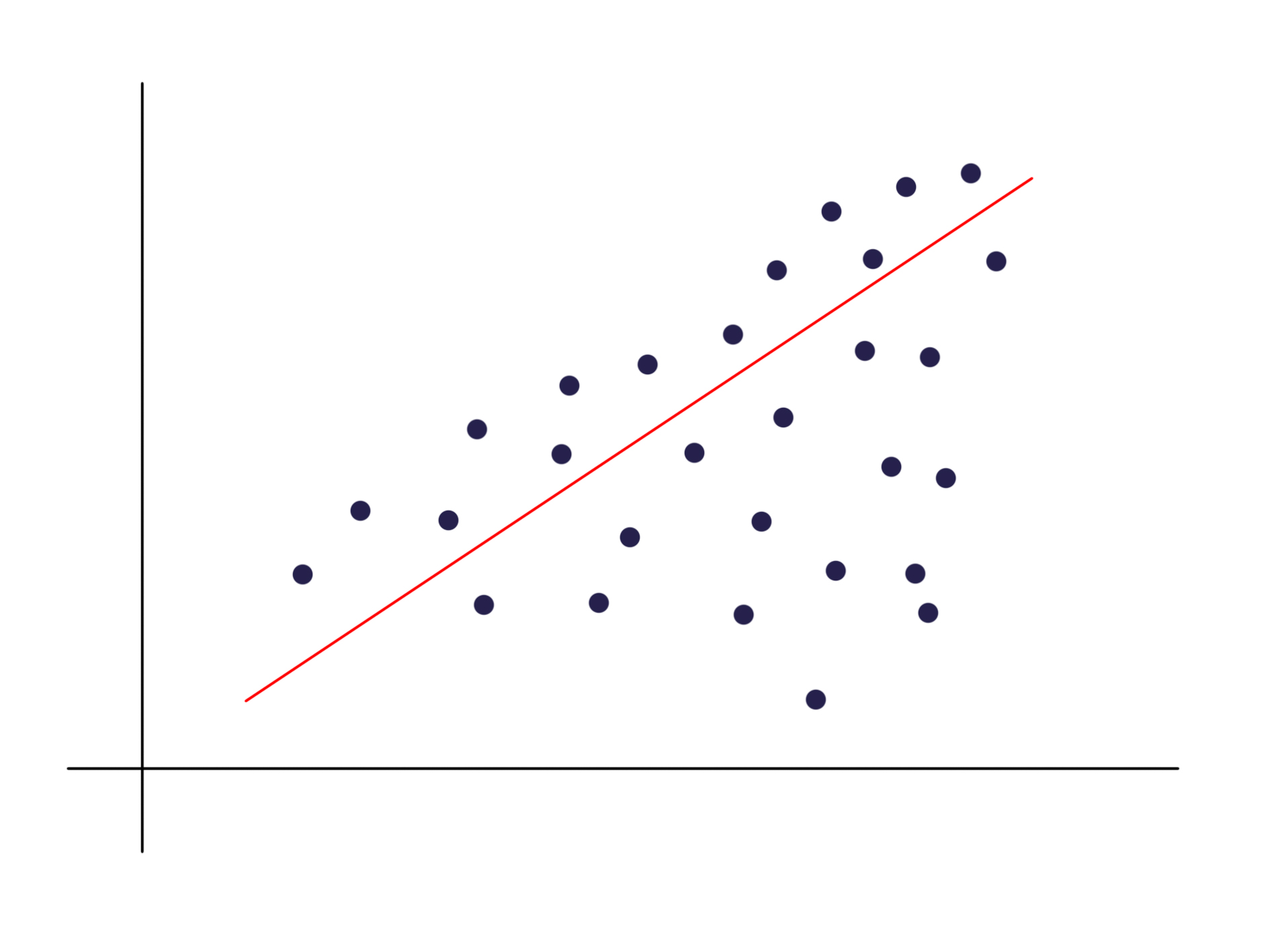
在分位数回归中也提到这种数据分布,分布会随着x的增大越来越分散,也就是说方差变大,虽然基于线性回归的算法我们也依然可以得到一条回归直线,但不能说回归效果很好,因为它并没有反映出数据越来越分散的特征,所以我们才需要分位数回归。那么这种数据分布和随机误差项有什么联系呢,一开始提到随机误差项表征数据因随机误差无法完美落在回归曲线上,假如我们基于这个数据集和我们得到的线性模型,针对两个小范围的x的数据,画出随机误差项的分布,就可以得到:
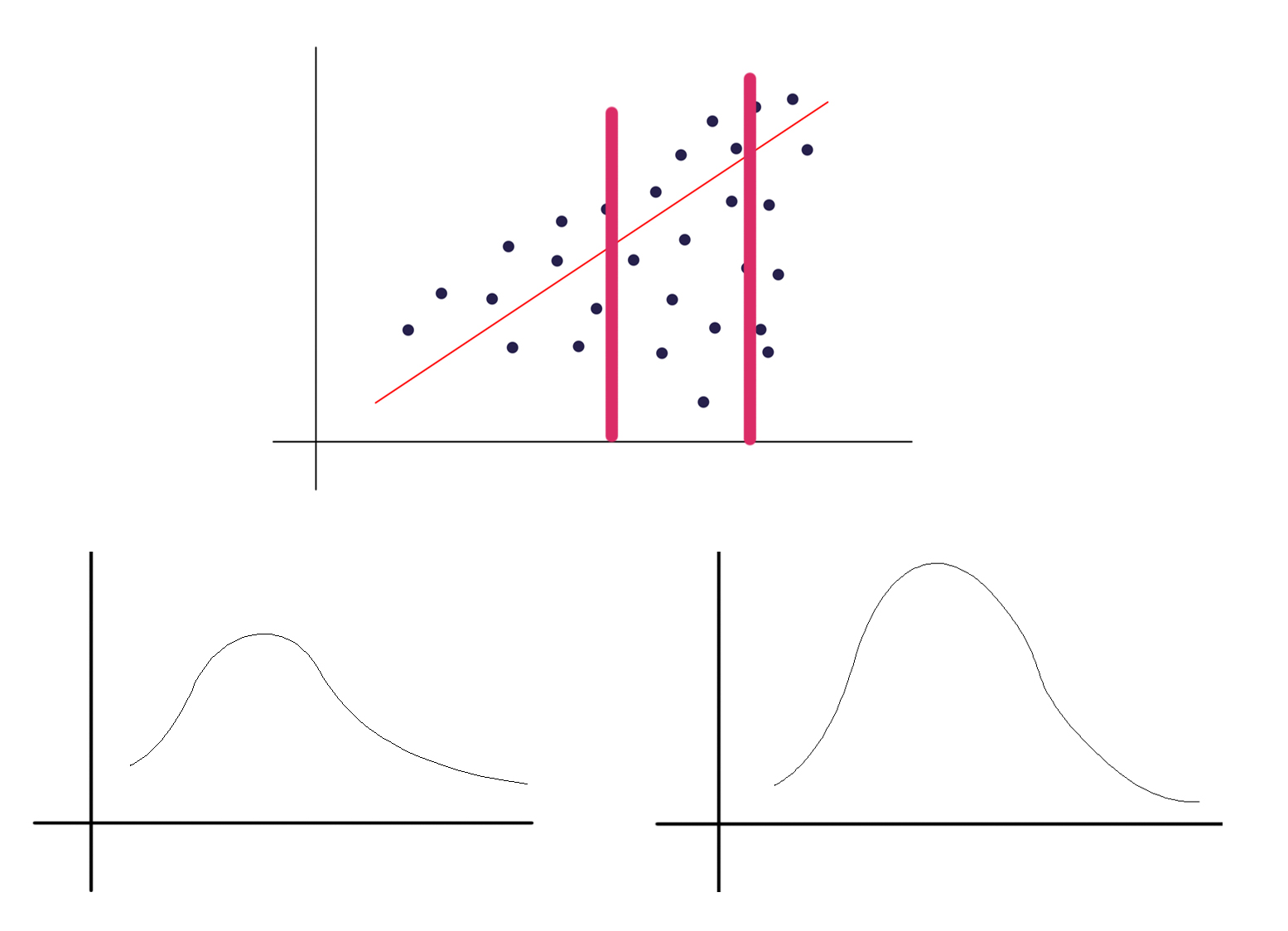
上图大概画出了两个范围的随机误差的分布状况(它们的均值都为0),可以看出,第一,随机误差的分布不是正态分布,第二,随机误差的分布的方差不是同一个数值。那么我们再回想一下,对于一开始提到的理想的数据分布,应该是数据对称地分布在回归曲线两侧,同时分散程度是接近的,这也就意味着,随机误差项服从正态分布,且独立同分布。
经过上面的论述,我们就知道随机误差项服从正态分布时模型的效果最好,而因为响应变量的随机性主要受到随机误差的影响,所以可以认为响应变量也服从正态分布:
其中,期望等于回归函数的输出(假设随机误差的期望为0),方差等于随机误差的方差
除此之外,我们还需要注意,在我们进行线性回归的时候,其实一开始就假设了解释变量和响应变量之间是服从线性关系的,假设他们之间不服从线性分布(以上图的数据分布为例),而我们依然采用线性回归,那么他们的残差就被模型认为是随机误差造成的,这也就导致了随机误差不服从正态分布。再回想一下,其实响应变量因为随机误差的存在才被认为是随机分布的,当随机误差不服从正态分布,响应变量也就不服从正态分布了。
上面的结论也说明了,虽然响应变量的分布和响应变量解释变量之间的关系是两回事,但是它们之间是相互联系的。
上面主要分析了线性回归要求响应变量服从正态分布才能有好的回归效果,这是第一个限制,第二个是要求响应变量和解释变量之间是线性关系,因为这两个限制条件,就导致了线性回归模型在有些情况下是不适用的,于是就有了我们的广义线性模型,它主要改进了线性回归的两个限制:不要求响应变量服从正态分布,以及响应变量和解释变量之间可以服从非线性关系。