逻辑回归(Logistic Regression)
线性模型可以用于回归学习,可是可以利用线性模型进行分类吗,答案肯定是可以的,只要利用逻辑回归就可以了。
逻辑回归是从线性回归推导来的,在介绍逻辑回归之前,先介绍一下广义线性模型的概念。所谓广义,就是更加通常意义上的线性模型,看回线性回归,我们可以写成另一种形式:
其中f(x)称为link function,在线性回归中f(x)=x,如果我们改变f(x),实际上就相当与对x的输出做了一个映射,如果我们引入特别的f(x),甚至能让线性变化的自变量获得非线性变化的因变量。
所以逻辑回归就是从link function入手,为了实现分类,把线性回归的输出空间控制在[0,1]之间,这样就可以把输出作为概率,解决二分类问题了。
我们需要的link function是对数几率函数(logistic function),logistic function也叫sigmoid function,提到这个sigmoid function又和神经网络有很大联系了,这里暂时不深究,它的形式为:
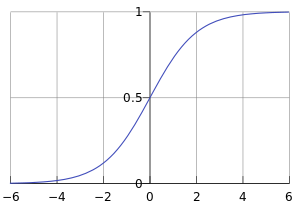
从图像就可以直观看出,不论自变量取什么值,输出都在[0,1]之间。
把sigmoid函数代进原来的线性方程中,得到:
来分析一下这个式子,首先要注意的是,我们对表达式做了简化,原来线性回归的表达式是:
可以看到,这里不是简单把ax+b代入sigmoid函数里面,而是选择了theta*x,这是一个简化,其实是在x里面增加了一个常数项1,这样就可以把b归入theta中了。另一方面,我们也做了假设:
同时有:
因为sigmoid函数的输出在01之间,所以这样定义是合理的,然后我们就可以把h(x)认为是输入属于1的概率,我们要知道,二分类样本数据的标签只有0和1,所以我们训练模型的目的,就是让标签为1的特征,在模型中输出的概率尽可能高,标签为0的特征,在模型中输出的概率尽可能低。根据这个特点,我们就可以定义损失函数了。
按之前的思路,我们完全可以定义MSE,
上面这个损失函数当然没问题,但是实际上是计算梯度将会十分麻烦(因为sigmoid函数求导有点复杂),所以这里提出另一种新的损失函数,也是逻辑回归中更常用的损失函数:
这个损失函数其实就是同时考虑了y等于1和0的情况,从函数的形式可以看出,损失函数越接近1,模型的效果就越好,和之前最小化损失函数的情况有点不一样。
为了进一步简化求解,引入log,有:
最后,对损失函数求和,得到针对整个模型的损失函数:
既然我们要让损失函数最大化,就可以利用梯度上升了,为了简化计算过程,直接得出梯度的表达式:
不要忘记,x是一个一维矩阵,xj是矩阵的第j个元素,对应第j个参数(theta)的项。
最后,我们就可以的得到theta的迭代公式:
以上就是logistics regression的全过程,得到模型之后,可以定义阈值:
这样,我们就可以根据阈值和概率,对y进行分类了。这里想要补充说明的是,我觉得这个阈值有点像模型的超参数,也就是我们训练模型改变的是参数,也就是逻辑回归中的theta,当我们训练得到最优的theta之后,才可以根据实际情况对超参数进行调整,看模型会不会得到改进。另一方面,阈值为0.5是一般情况下的取值,如果输入数据十分不平衡,需要根据实际情况调整,具体来说,就是根据上面说的,可以随便选一个初始阈值,训练得到最优参数,调整阈值,再训练,重复这个过程,得到最优阈值和最优参数。
最后再强调一下,虽然我们通过sigmoid function将线性输入的输出变成非线性的,局限在了[0,1]之间,但是本质上逻辑回归还是一个线性模型。假设我们选择阈值为0.5,有:
也就是说,到头来我们只是通过变量x和权重w的线性组合去判断分类结果。所以本质上还是一个线性分类器。
线性回归和逻辑回归都是线性模型,为什么我们一般采用逻辑回归做分类,事实上,我们也可以用线性回归做分类,可是因为线性回归模型受离群点影响较大,或者说对分类特征十分明显的数据,会对模型造成明显影响。
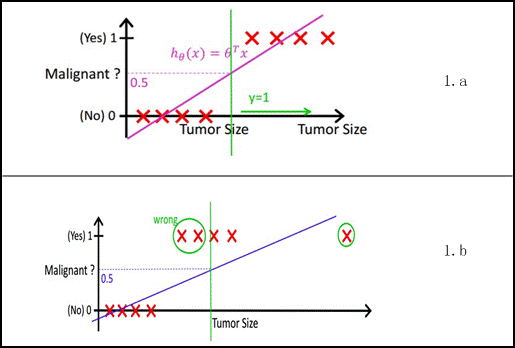
而逻辑回归,因为sigmoid函数的特性,在输出为01附近逻辑曲线是十分不敏感的,这就意味着逻辑曲线对刚刚提到的离群点具有更强大的包容性,或者专业地说,就是模型鲁棒性更强,所以我们选择逻辑回归就是为了这个优点,而不是说通过一个sigmoid函数把原来做不了分类的线性回归变成了可以做分类的逻辑回归。因此,一般情况下,逻辑回归的分类边界是一条直线。为什么说一般情况,正如线性回归,我们同样也可以在特征工程中,引入新的特征(比如引入一个x^2),把分类边界变成曲线,更好地对数据进行分类,至于怎么找到合适的新特征,就是特征工程的工作了。