判别分析

关于分类问题，之前已经介绍了logistic回归，常用于解决二分类问题，多分类当然也可以，但是需要进行一些改进，这里就介绍一个另外一种新的算法，判别分析，常用于解决多分类问题，因为多分类的情况比较复杂，但也是在二分类的基础上进行改进的，最重要还是理解判别分析的思想。所以这里还是主要介绍判别分析在二分类问题的应用。

判别分析可分为线性判别分析和非线性判别分析，具体的集中判别分析方法有距离判别法、Fisher判别法、Bayes判别法和逐步判别法。

首先我们来了解一下距离判别法，这是最简单的判别方法，主要就是根据已知分类的数据，计算出各个分类的重心，再根据新样本到各个分类的重心的距离去判断它属于哪个分类。

然后是fisher判别分析，我们主要介绍一下针对二分类的fisher判别分析，它思想非常朴素：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、不同类样例的投影点尽可能远离。在对新样本进行分类时，将其投影到同样的这条直线上，再根据新样本投影点的位置来确定它的类别。比如下图：
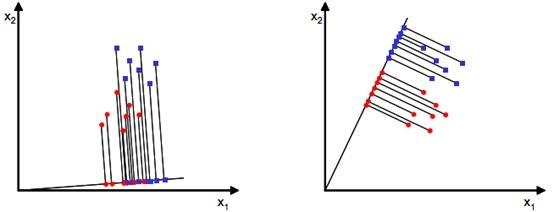
ポジショニングマップ
可以看到，这里有两个类别，两个特征x1和x2，现在投影到w就变成只有x上的一个点了，而对比两幅图，可以看出右图的分类效果更好，虽然看起来是这样，但是我们应该怎么用数学的语言定义效果更好呢。

简单来说，有两个方面，第一，两种类别的样本在w上的投影尽可能分离，距离尽可能远，这里我们定义样本的均值（中心点）：
$$\mu_i = \frac{1}{N_i} \sum_{x \in \omega_i} x$$
投影到w之后，样本的均值就变成：
$$\mu_i' = \frac{1}{N_i} \sum_{y \in \omega_i} y = \frac{1}{N_i} \sum_{x \in \omega_i} w^Tx = w^T\mu_i$$
我们希望两种不同类别的样本尽可能远离，其实就是两个样本的均值之间的距离尽可能大，但是只考虑这个情况也不足够，比如：
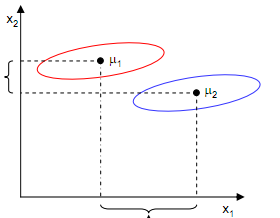
ポジショニングマップ
在这里，如果指按照让两个类别的样本的均值尽可能远离，那么实际上我们也不能对样本进行完美的分类，我们还需要考虑样本投影到w之后的分散情况，也就是投影后的样本的方差，方差越大，样本之间就越难分离：
$$S_t^2{'} = \sum_{y \in w_i}(y - \mu_i')^2$$
总的来说，我们判断向量w的分类效果好不好，主要看样本在w的均值和方差，把这两个合并在一起，可以构建度量公式：
$$J(w) = \frac{|\mu_1' - \mu_2'|^2}{S_1^2{'} + S_2^2{'}}$$
只要我们使得J(w)尽可能大，就能同时满足均值差尽可能大，而方差尽可能小了。通过这个过程就能求出最优参数，到最后，还是机器学习那一套过程。

针对多分类的情况，依然把样本投影到一维向量可能是不可行的，假设我们有c个类别，需要k维向量（基向量）来做投影。