非参数回归之核回归
之前介绍了loess,现在继续了解一下核回归这个非参数回归方法。
整体来说,核回归和loess有点接近,但又有点不同,首先,loess对于在x0估计y的取值,它会选择划定一个范围,通过该范围的样本去估计x0的y值,但是核回归不一样,它会考虑选择全部样本去估计这个x0的y值。另一方面,loess在估计关于x0的y值,计算各点的权重需要先计算距离再通过权重函数计算,而loess则直接把核函数作为权重函数,因为核函数本身也可以作为概率密度函数,所以省去了loess中的归一化等处理,简化了过程。
下面我们选择高斯核函数,用一个具体的例子说明核回归的思想。
高斯核函数和正态分布函数一个样,呈一个钟型曲线,这样,假如我们把拟合点x0作为高斯核函数的期望,就可以直接得到样本的各个x在高斯核函数的取值作为它们的一个权重。
以上的过程,对应loess中的决定拟合点的数量和位置,确定关于各个拟合点的各个样本权重(因为我们采取所有样本进行估计,所以不需要选择每个拟合点附近距离最近的n个点这个步骤)。
接下来就是loess中的拟合步骤了。在loess中,我们可以进行一次或者二次的多项式拟合,而在核回归同样也是这样(不过一般在核回归中采取零次或一次),首先写出核回归的d次多项式:
这个拟合的d次多项式是比较特别的,可以看到系数对应的是x_i - x而不是单纯的x,另一方面,关于权重函数,同样也是用x_i - x:
当然,不论是拟合的多项式还是权重函数,自变量都是x,但是写成x_i - x,我认为这是为了反映出比起自变量x的位置,x与其他样本点才是更重要的,更能反映出权重和拟合的多项式的关系的变量。换个角度来思考,我们现在做的是非参数估计,没有做关于总体分布的任何假设,全部的分析都是基于样本进行的,所以其实我们做出来的估计都是基于样本的,在这个角度看来,如果我们要估计某一点x的取值,比起它所在的绝对坐标,它和其他样本的相对坐标才是分析它的取值的关键,这是我认为多项式和权重函数都采取x_i - x作为自变量的原因。
分析了核回归拟合的多项式之后,下一步就是分析怎么解出多项式的参数beta了,可以知道,我们的目标就是拟合一个多项式,使得多项式尽可能地拟合附近的样本,所以和loess一样,这里也是采取局部线性回归的方式,结合权重定义损失函数:
使损失函数达到最小,就能得到得到参数。
就像前面提到的,核回归的拟合多项式一般取零次或者一次,也就是d=0或者d=1,针对这两种情况,我们可以解出各自的最优参数表达式,并重新代近拟合方程,得到各自的表达式:
第一条式子对应d=0的情况,也称为Nadaraya-Watson kernel estimator,第二条式子对应d=1,也称为local linear kernel estimator
关于拟合多项式选择零次和一次的区别,下图会更清晰地反映出来:
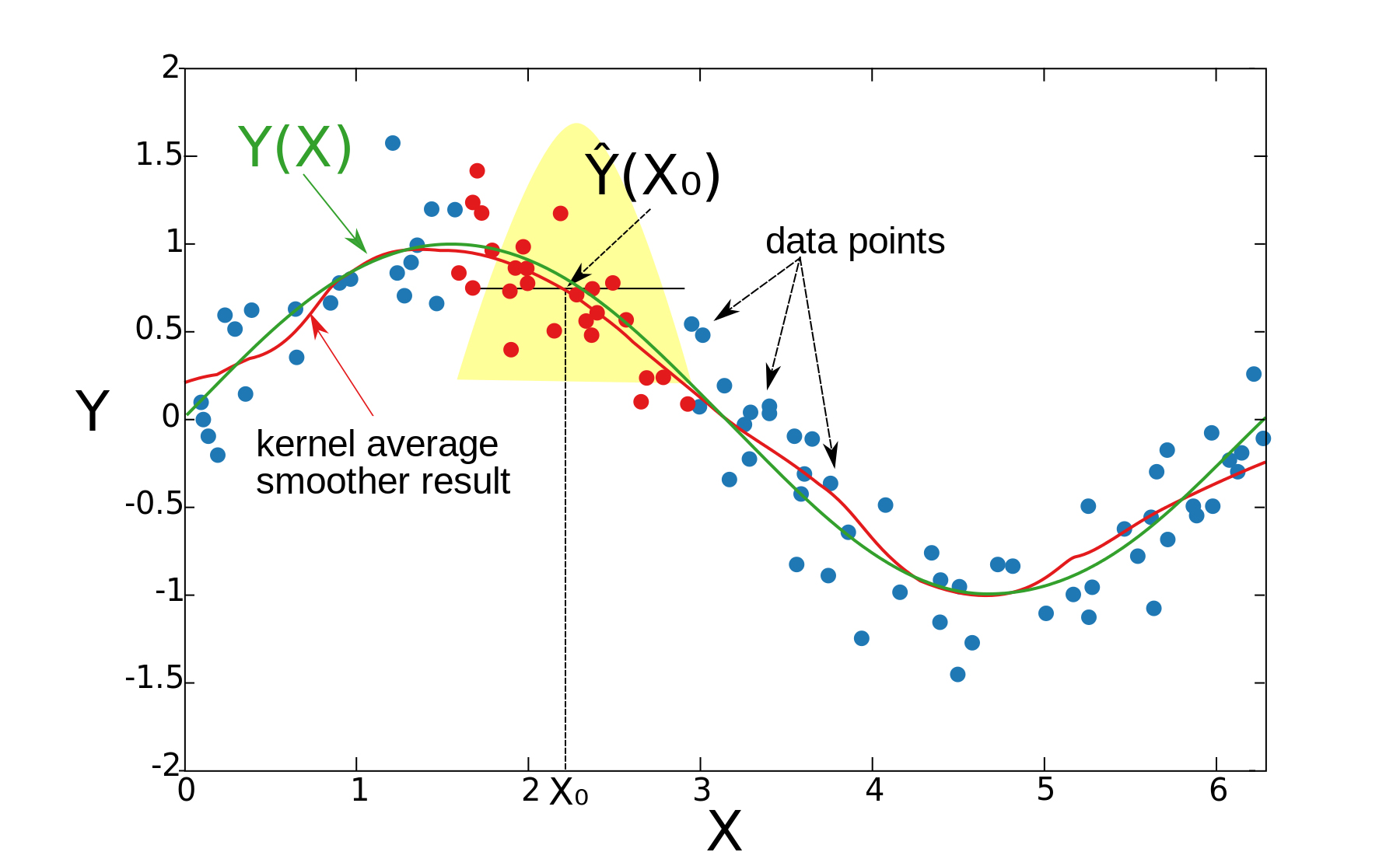
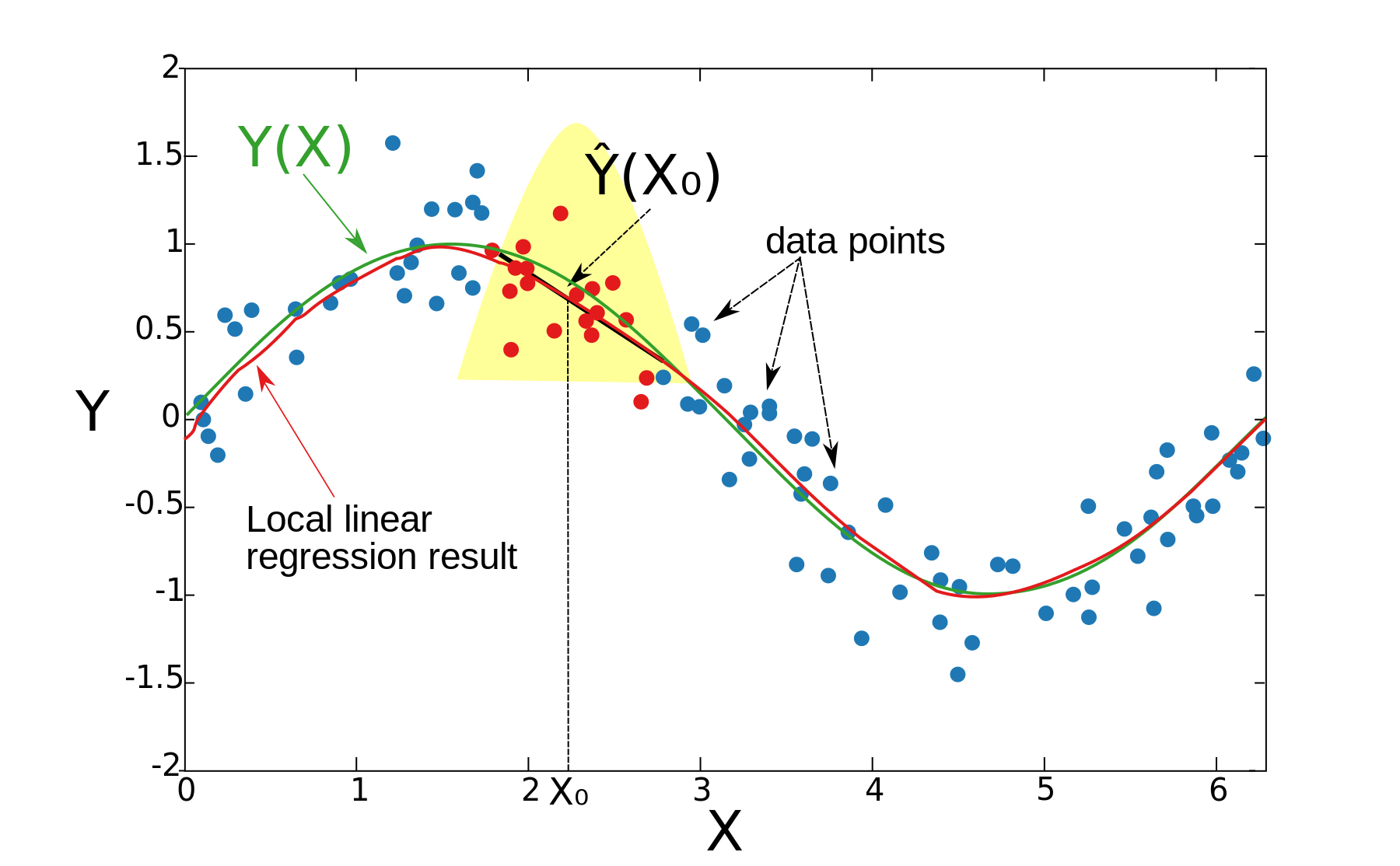
从上图可以看到,Nadaraya-Watson kernel estimator对拟合点拟合的结果认为这个区间的y值都是常数,所以是一条水平的直线,而下图则拟合出一条倾斜的直线,更接近真实的情况。但是必须说明的是,我们要做的不是像loess那样在一个个小区间拟合出一条直线再整合,我们在核回归中要做的是通过拟合多项式从而估计在拟合点x的取值y,我们要估计的是在拟合多项式上的一个点。