EM算法
EM算法(Expectation-Maximization)用于存在缺失数据的参数估计,比如说,现在我们进行最大似然估计,寻找θ使得p(y_obs|θ)最大,但是有部分数据没有被观察到y_mis,EM算法的思路就是:首先,定义条件期望:
这一步是E-step,接下来是M-step,更新θ:
不断重复这两个步骤,直到收敛。
说实话,我是看不懂上面的算法,所以还是从最简单的例子开始慢慢理解它。
假设现在有硬币a和b,要估计他们抛到正面的概率,试验过程可以是a和b轮流随机分别抛十次,比如第一次是a抛了十次,第二次是b抛了十次,第三次是b抛了十次,最终一共抛了一百次。然后根据试验结果进行极大似然估计。
现在我们考虑这样一种情况,假如现在我们抛十次,只有前五次观察到具体是谁抛的,后面五次却不确定抛的是A还是B,那么我们怎么办,当然我们可以只用观察到的前五次进行分析,但是本身数据量就少,还要丢弃那么多数据,就显得有点浪费了,所以这时候我们就需要EM算法了。
EM的主要的思路就是,先假设a、b抛到正面的概率,比如a是0.2,b是0.4,然后再分析缺失数据,猜测这个数据最有可能是a还是b抛出来的,比如第六次实验,抛出了三次正面七次反面,抛到正面概率比较低,再看看我们的假设,a抛到正面的概率比b低,所以就假设第六次实验是a做的,然后继续猜测第七次、第八次等等。
猜测完了,我们就得到完整的数据集了,就可以利用MLE估计了,最后估计了结果是a为0.35,b是0.65,还没完,因为这是根据我们一开始的假设求出来的参数,我们需要把这个估计出来的结果作为新的假设,重复上述步骤,再猜测每次缺失的试验是a还是b做的,然后再用MLE估计,不断重复,直到最后两次估计的结果之间的差异足够少(也就是收敛,这是认为设定的,比如差异小于0.001),就认为这个参数就是我们要求的结果了。
现在有一个问题,我们随便找了一个概率作为ab 的估计概率,那么它最后收敛的一定就是真实值吗,答案是不一定的,具体来说,迭代过程会使得参数不断接近真实值,但是不一定最后的结果就是真实值,有可能是在达到全局最优之前就碰上了局部最优无法逃脱,所以初始点很重要。
还有一个问题,在原算法中我们求的是条件期望,为什么?这涉及到对我们上面介绍的例子的改进。
上面的例子中,在估计缺失的数据到底是A还是B抛的时候,我们应用了极大似然估计,根据结果分析出A抛出试验数据的概率和B抛出试验数据的概率,然后选择概率较大的那个认为本轮试验就是它做的。但是,我们可以进一步利用这个两个概率,认为本轮试验有a%的可能是A做的,有b%的可能是B做的,这样做的意义是什么?首先,就是可以充分利用数据,因为上面的做法如果我们选择了A就抛弃了B的数据,这里我们则把全部数据都利用起来,第二,我们因为利用全部数据,所以不需要比较A还是B更接近试验数据,简化了过程。
具体来说,就是根据极大似然估计计算每一次试验AB抛出试验结果的概率a%和b%(实际上就是1-a%),然后,我们也会有AB抛正面的概率,根据这些概率,就能得到每次试验,抛出来的正面和反面,来自AB的概率,下图会更容易理解:
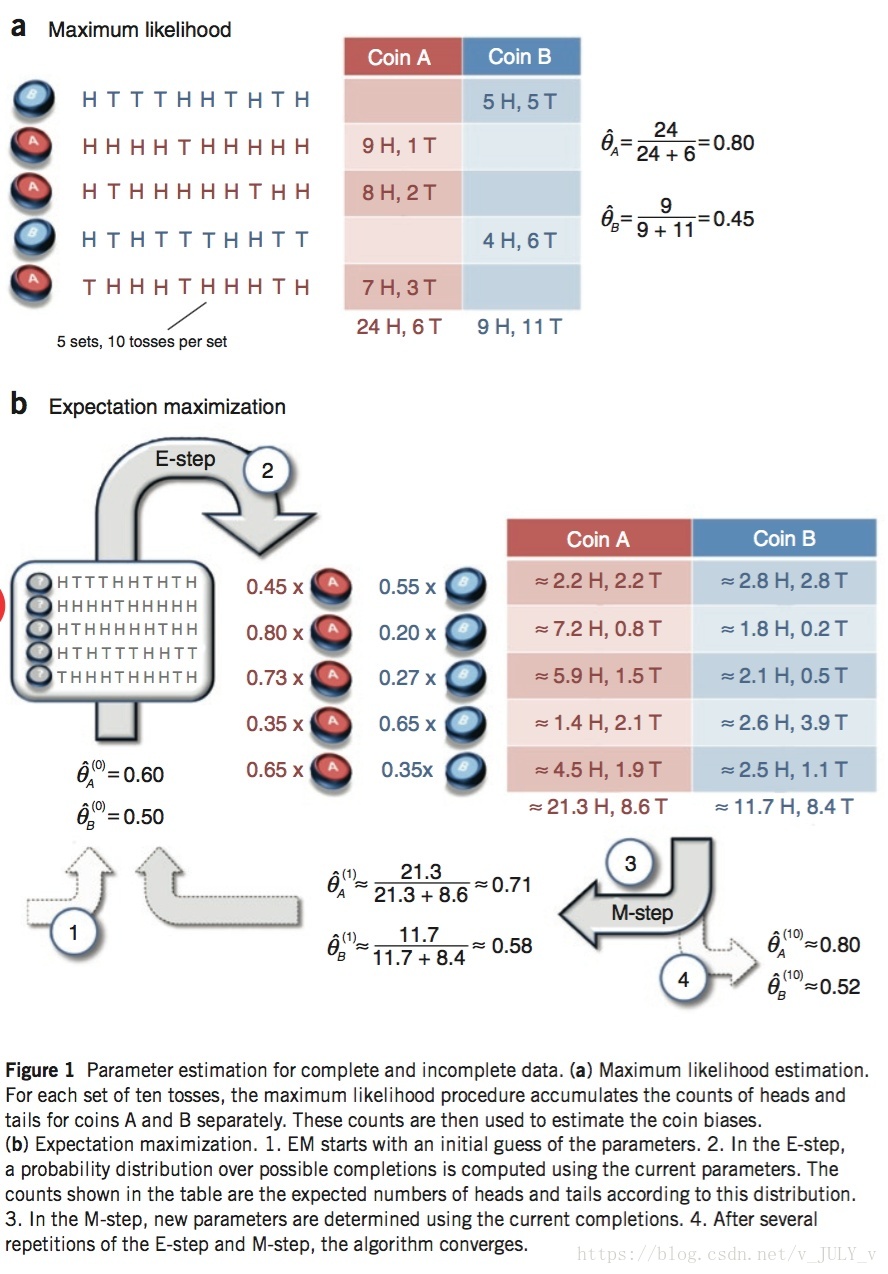
图中的数据和我描述的有点不一样,但本质都是一样的,它列出抛中的正面和反面根据概率是来自AB的次数,所以可以看到,每一次试验抛十次,五次正面五次反面,根据概率其中2.2次正面来自A,2.8次正面来自B,2.2次反面来自A,2.8次反面来自B,加起来就是总数10,对每一次试验都算出这个值,最后计算期望,通过期望反映A抛中正面的概率是多少,B抛中正面的概率是多少。
再总结一下,改进的方法和原来的方法有什么不一样。最主要的,就是简化版本,我们首先随机找一个参数初始值,上面这个例子就是AB抛到正面的概率,然后现在试验数据缺少了到底是A还是B抛的,所以就根据这个概率,和试验的实际情况,猜测这次试验是谁抛的,说实话,比如抛十次八次正面,然后猜测A抛到正面的概率比B高,直接就可以认为是A抛的都不用做什么计算了,可能其他情况需要吧,但是这里猜测了,就可以填充数据,最后就正常的用极大似然估计估计参数,用新参数替换初始值,继续重复直到收敛。这个方法的问题就是我们猜测了是A抛之后,就不要B的数据了,所以就有人想到,还不如AB的数据都要,换成用概率或者说比例表示,每次试验,正面反面分别有多少来自于AB,每次试验都这样算,最后就得到一个总的结果,算期望,其实就是做一个归一化处理,把结果归一化到[0,1]区间内,这样做,因为充分利用了所有数据,所以就比一开始的简化版本,在每一次迭代得到的参数估计更接近真实参数值,不得不说,想到这种方法的人真的厉害。
以上就是EM算法的思路分析,虽然这个算法用于数据缺失的情况,但是感觉还是有一定的限制,比如这里就主要用在极大似然估计,而且数据还不是一组数据全部信息都缺失了,只是缺失了其中一个,主要根据这组数据的其他信息补全这个缺失的信息,所以还是挺科学的,但是如果整组数据都没了,能不能通过其他组数据补充,暂时我不知道,但是说实话,既然整组数据都没了,应该也没必要想办法估计出来了吧,本身就是估计就不准确了,即使估计出来,最后也会影响模型的结果吧。