概率密度估计
概率密度估计可应用于无监督学习、特征工程、数据建模,解决这个问题的方法包括参数估计和非参数估计。
简单来说,参数估计就是假定数据是符合某一种特定的性质或者分布,然后我们再去估计这些性质或者分布所需要的参数,但是因为这种假设和实际往往有较大的差距,所以很难得到令人满意的结果。而非参数估计,比如接下来介绍的核密度估计,它是不利用数据分布的先验知识,不进行任何假设,直接从数据出发进行研究估计的方法。
直方图是一种基础的数据可视化方法,定义组距和组数,然后对每一组的数据进行统计,最后均一化处理让总面积为一,即可得到密度直方图。组距有点像核密度估计中的带宽,在这里它反映了区间范围的取值,如果取得太大,平均化的作用就会突出,这样密度的细节就会被淹没,而变成一条普通的柱子,太小又会受随机性影响太大,而产生不规则的形状。于是怎么选择组距就又成了一个问题了。
除此之外,直方图还有一些缺点,我们这样把数据划分成一组组,数据就不是平滑的了,得到的图像也会随着组距的不同而改变,所以直方图不是唯一的,这样不同的数据对比起来就很困难了,另一方面,直方图也没办法处理极值的问题。
为了解决直方图的这些问题,就有了核密度估计。首先什么是核(kernel),在非参数估计中,核是一个函数,用来提供权重,例如高斯函数就是一种常用的核函数。核密度函数的思想,其实就是如果某一个数在观察中出现了,我们可以认为这个数的概率密度会比较大,和这个数接近的数的概率密度也比较大,而离这些数比较远的数的概率密度就会相对小一点。
基于这种想法,针对观察中的第一个数,我们可以用核函数(比如高斯函数,就是正态分布的函数)去拟合我们想象中的那些近大远小的概率密度,然后对于第二个、第三个等等的数都采取这种方法,得到多个概率密度函数,再取平均,这样的结果,首先,它也是一个连续的函数,其次,因为当某个数出现次数较多,它的概率密度函数的最大值出现在那里的次数也多,所以平均下来那个位置的密度函数值也会更大,所以得到的平均密度函数可以反映出数据的密度分布情况。
我们可以考虑一种情况,假设现在有一个核函数,它是这样的,假如一个数据在一个限定的区间范围内,概率密度为1,在区间范围外,概率密度为0,然后这些区间是我们在数轴上分割的一个个不重合的区间,那么,我们应用这种核密度估计出来的密度函数会是什么样子的,答案就是我们的直方图。所以说,事实上,核密度估计就是直方图的扩展,具体来说,是对直方图进行了平滑处理(smoothing),直方图之所以直,是因为它的核函数的值是离散的,是我们把这种离散的核函数换成了连续的核函数,再通过相同的累加、加权平均,得到整体的密度函数的估计,这时候新的密度函数就是连续的了。顺带一提,关于直方图和核密度估计一个很重要的区别是,直方图我们是一开始就决定了区间是怎么划分,决定了核函数的位置,然后我们只是把数据放到某一个核函数,或者说某一个箱子里,可是对于核密度回归,我们是先有数据,然后再根据数据的中心位置决定我们的核函数的位置。
核函数的选择有很多,但是都必须满足一个条件,那就是在数据点处为峰值,曲线下面的面积为1。
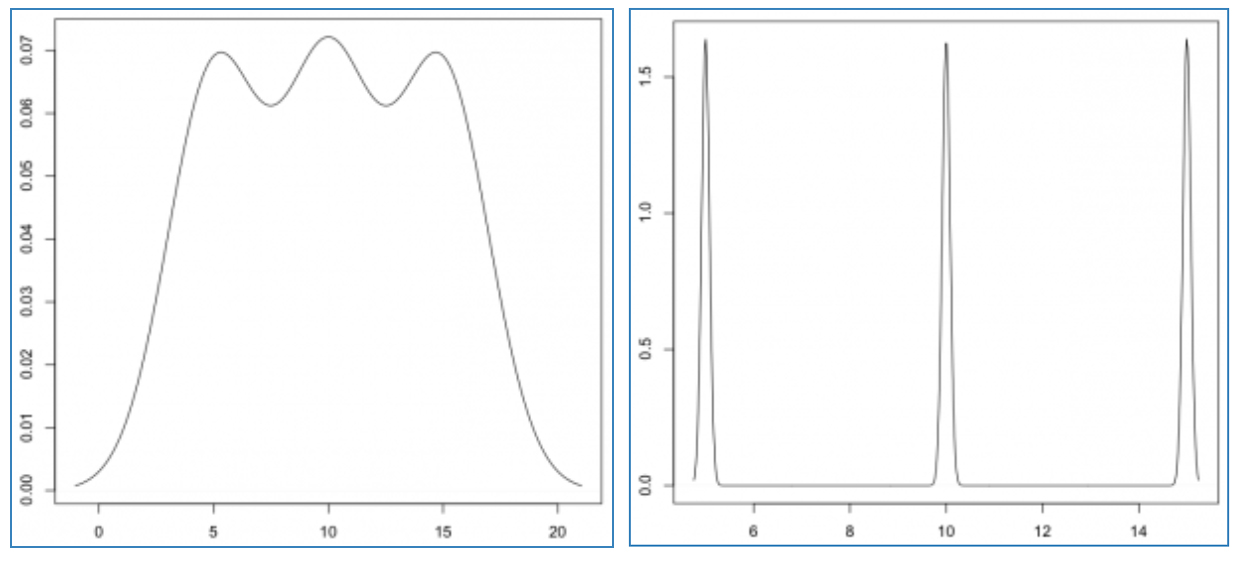
关于核密度估计还有一个需要注意的地方,那就是带宽的选择,带宽就是反映我们的核函数近大有多大,远小有多小,比如我们选择高斯函数,带宽小的话,我们的函数图像就是很陡峭,主要集中在峰值附近,这样最后得到的平均密度函数的图像可能也会是一个个峰值的形式,不大连续,可是如果我们加大带宽,那么平均密度函数的曲线就会更加平缓。
那么我们应该具体如何选择带宽呢,一个通用的办法就是最小化AMISE(Asymptotic Mean Integrated Squared Error),首先是MSE(Mean Squared Error),它等于偏差加方差
可以看到,h很小时,第一项很小,MSE主要由方差构成,h很大时,第二项很小,MSE主要由偏差构成,所以方差偏差是成反比的。
MSE只说一个点的误差,对样本空间进行积分就能得到所有点的均方误差和:
化简并去掉高阶项后,就能得到AMISE:
为了得到使AMISE最小的h,对上式求导等于0,就能得到最优h,但是,因为其中包含了未知函数f'',所以只能作为理论讨论,同理,直方图的最优组距也可以通过这个过程进行推导。换个角度来说,从一开始我们就不知道真实的概率分布函数,当然我们也不可能得到最优的估计了,一切的分析都是基于我们的观察数据进行的,都没有真实值,哪来的误差。
参考资料:
[1]https://blog.csdn.net/pipisorry/article/details/53635895
[1]https://blog.csdn.net/pipisorry/article/details/53635895