决策树
决策树是一种分类模型,如下图:
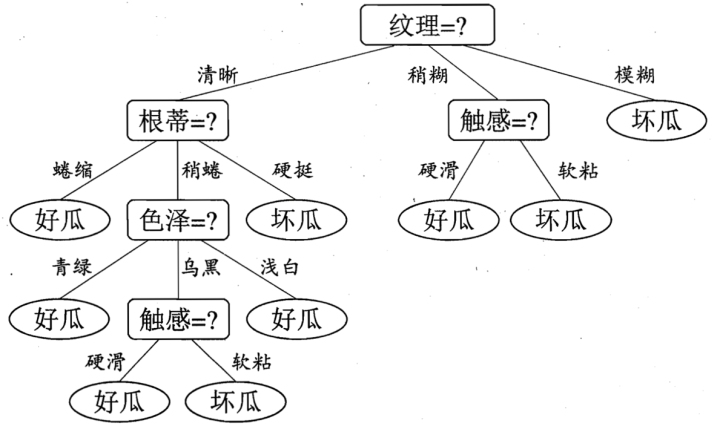
根据这棵树,我们就可以一步步进行判断。而本文讨论的重点就是如何构建这么一棵决策树,简单来说,构建一个决策树包括三个过程:特征选择、决策树生成、决策树剪枝。
特征选择就是判断对于当前的节点,我们选择用哪个特征,比如上图的最上方选择用纹理作为根节点,那么到底是怎么分析出来的呢。事实上,特征选择的方法有很多,对于不同的方法,也衍生出不同的决策树,比如比较常见的通过信息增益选择特征,对应的决策树叫ID3,通过信息增益比进行选择,对应的就是C4.5,通过Gini指数选择的就是CART。
在我们正式讲解ID3的细节之前,首先来了解信息增益、熵、条件熵这些概念:熵表示的是随机变量的不确定性,条件熵表示在一定条件下随机变量的不确定性,而信息增益则是等于熵减去条件熵。通俗地说,就是如果给定一个条件,那么熵会减少多少,从这个角度来说,或许我们用熵减去信息增益等于条件熵这个公式更好理解。
因为我们都希望熵或者条件熵尽可能小,所以信息增益当然就越大越好了,如果信息增益越大,就意味着给定一个条件之后,熵也会大幅度减小,很明显这个条件就是我们希望得到的特征,所以我们可以通过信息增益去进行特征选择,构建决策树。
我们可以通过公式计算信息增益:
知道了如何计算信息增益之后,再来看看如何进行特征选择,如何确定出决策树的第一个节点,首先,我们要计算所有特征的信息增益:

可以看出,纹理的信息增益最大,所以我们选择纹理作为第一个节点(根节点)。根据纹理,我们可以把原始的数据集分为纹理清晰、烧糊、模糊三个子类,在这三个子类的基础上,我们可以判断一下,每个子类的纯度如何,比如90%都是好瓜或者坏瓜,就可以停止分析了,否则,就继续前面的步骤,继续进行特征选择。
所以对ID3来说,整个构建决策树的过程,就是自上而下的,一步步确定每个节点(特征),从而使得每个子类的纯度都足够高,这个过程就是决策树的生成过程。事实上,所有的决策树都是依据这样的构建过程,唯一的不同就是特征选择的依据。
接下来,我们来看一下信息增益的问题(有不足是正常的,不然也不需要其他判断依据了),如果一个特征可取值较多,比如现在有一个特征是编号,那么结果就会更偏向于它。因为可取数值较多,就会导致每一个取值的子集较小,在计算过程中,模型会认为条件熵较小,从而推导出信息增益较大的错误结论。
既然子类太多也不好,那么在信息增益的公式中,引入惩罚项不就行了。我们希望信息增益增大,但又不希望特征的类别数过多,那就对信息增益除以一个和特征类别数有关的项,这就是c4.5算法,改进的信息增益公式就称为信息增益率公式:
可以看到,IV(a)和类别数成正比,所以信息增益率就不会盲目朝着类别数更多的特征进行选择了。
以上就是ID3和C4.5的基本思路,除此之外还有cart,这里就暂时不细说了。总的来说,不论选择哪一种决策树,目的还是希望分出来的子类纯度高一点,分类的效果好一点。
关于特征提取,再补充一点,上面提到的特征,可以看到其实都是离散型的,实际上还会有连续型的,比如一个瓜种植的天数,那么我们对这类特征进行选择的时候,其实还需要考虑对这个特征分成几个类别,每个类别的阈值用哪个,分出来的子类纯度更高,更具体的细节,这里就暂不细说了。
虽然生成一棵决策树是一个关键的过程,但也不能忽略了生成之后对决策树的评价和改善,最主要的考察就是这棵决策树会不会过拟合数据,因为有时候可能会生成太深的决策树(也就是节点过多),这时候子类的的纯度当然很高,但是拿去做测试的时候就发现这个模型的准确率不行,这就是过拟合的问题。一般来说,我们会通过剪枝,也就是删除部分节点,避免决策树过拟合。
综上所述,个人觉得,决策树是一种十分接近人的思维的模型,所以很容易解释,建模和测试模型的速度也很快,不需要做什么复杂的运算,但是很容易发生过拟合,优点缺点都很明显吧,算是可以看到天花板的模型。