聚类及K-mean算法
首先什么是聚类,和分类有什么区别,这里讲一个例子,比如有一群学生考完期末考试,现在要根据他们的成绩把他们划分成几个小组,让老师分别进行辅导,这时候,你不知道要划分几个小组比较好,但你可以根据他们的成绩,比较成绩接近的归到一个小组,这个过程就是聚类,另一种情况是直接给出了90分段的一个小组,80分段的一个小组,其他一个小组,根据这些要求把学生分组,这就是分类。
所以分类和聚类有什么区别呢,就是分类会有一个分类标准,或者说分类数据会有一个label,你可以根据label建模,也就是有监督学习,但是聚类没有一个前提标准,数据没有label,但会有一个聚类结果的评价指标,那就是簇内距离小,簇间距离大,其实这个和主成分分析有点相似,用pca的话来说,就是希望簇内方差小,簇间均值差异大。
接下来就讨论一下kmean算法,基本流程是这样的,首先我们要假设一共把数据分成k个cluster,假设为3,然后我们就从所有点中随机选三个点,然后计算其他哪些点和他们的距离最近:
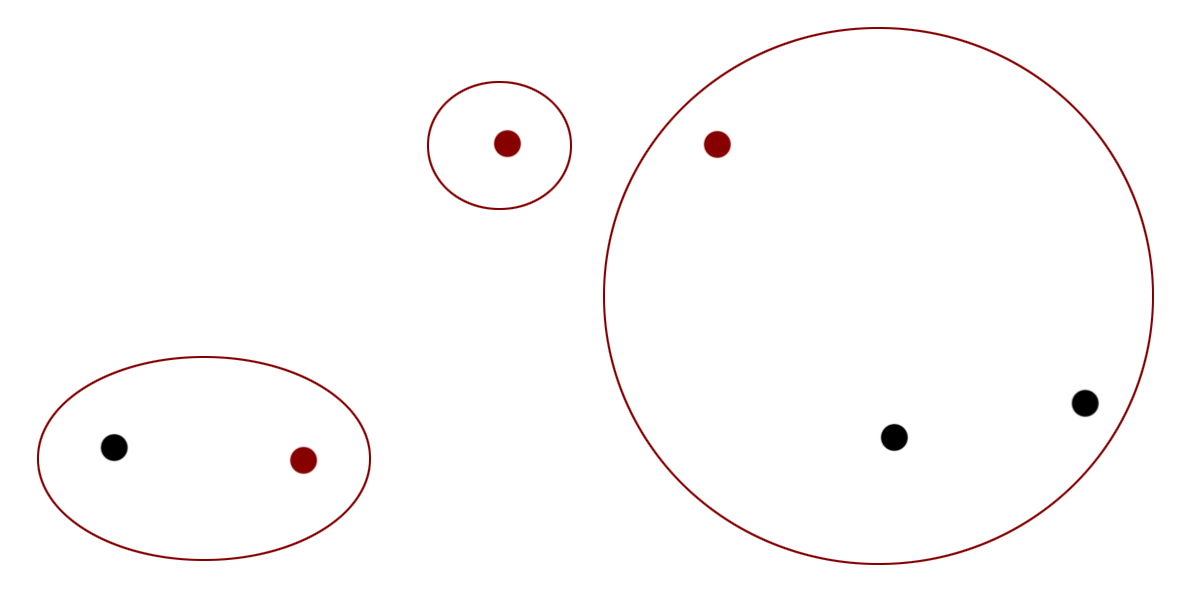
这是初步的聚类,可以看出,其实初始点的选取影响不少,如果选得好,直接就出结果了,不过选不好没关系,接下来,我们会通过计算三个cluster的质心,并通过计算各个点到这些质心的距离重新进行聚类:
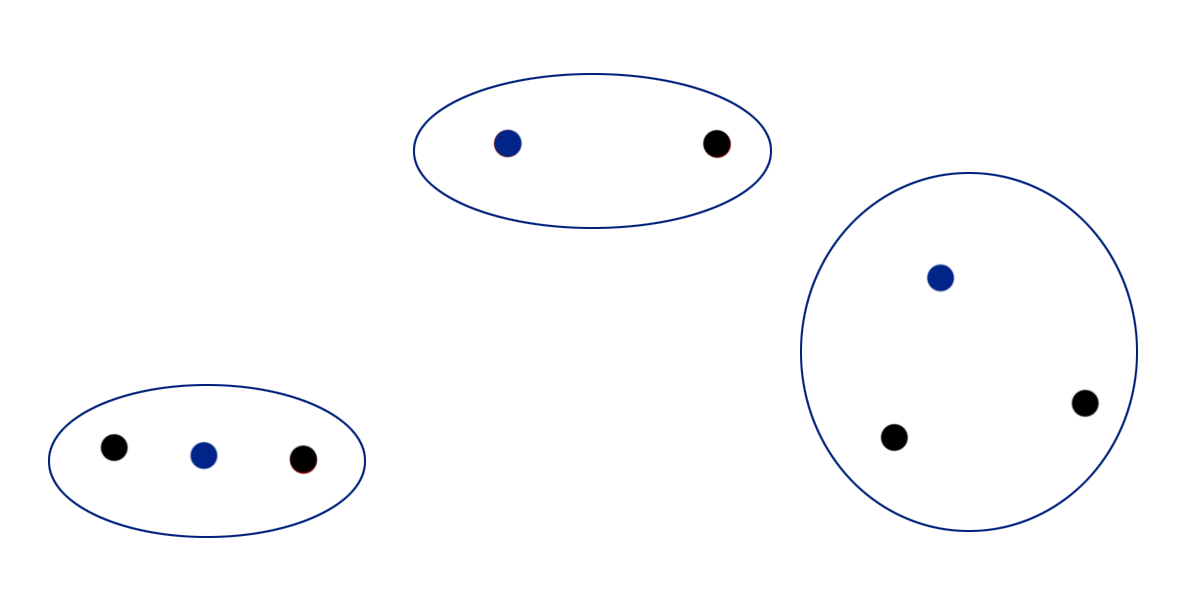
可以看到,第一次聚类中有一个cluster只有一个点,所以这个点也称为了新的cluster的质心。而从结果来看,经过两次cluster,其实就已经得到满意的结果了,那么对程序来说,它又是怎么知道什么时候结果才是满意的呢,那就是当两次迭代的质心都一样,想象一下,我们再继续做两次聚类分析,聚类结果也不会变,所以cluster的质心也不会变,因此这时模型就知道是时候停下来了。
以上就是聚类以及k-mean的基本思想,理解起来还是挺简单的,但接下来我想结合一下EM算法,分析两者的关系。
之所以联系到EM算法,其实是因为两者的过程其实十分接近,EM算法的一个应用场景就是数据缺失时的参数估计,首先就是猜出缺失的数据是什么,然后进行参数估计,再根据估计的参数重新猜缺失的数据,再估计,不断重复这个过程,直到两次迭代估计的参数差异足够小,就认为模型已经收敛,整个过程其实和k-mean是一样的:猜cluster质心,评估,重新计算质心,再评估,重复这个过程直到两次质心不变。
在网络上还有更多关于EM和k-mean关系的分析,这里暂不深究。