循环神经网络
如果说卷积神经网络是为了解决图像识别而提出的,那么循环神经网络(Recurrent Neural Network)就是为了解决自然语言处理(序列数据)而提出的,当然实际上这两种神经网络的用途很广,但是从自然语言处理的角度去看待循环神经网络可以更容易理解它的特性。
自然语言处理(Natural Language Processing),简单来说就是让计算机理解人类的语言,从而解决相关的问题,比如现在有一句话"我上班迟到了,老板批评了__",如果要填入最后一个词,我们很容易就能猜出是"我",可是怎么让计算机也能解答同样的问题,这就是自然语言处理要研究的。一般来说,我们判断最后一个词是什么,是根据前面给出的句子来判断的,循环神经网络为了解决这类问题,就提出可以把整个句子看成一个离散时序序列,先对句子进行分词,然后按顺序输入到模型中,最后根据前面的输入判断应该得到的输出,为了满足让后续的输入在分析过程中能够"记住"前面的输入,循环神经网络在一般多层感知器的基础上,在隐层添加了多一个神经元作为缓存单位,用于保存该时刻隐层的输出,这样在下一个时刻,隐层就能读取该神经元的数据,达到分析历史数据的效果。
上面的描述的就是最简单的一种循环神经网络,单向RNN,可以看出,实质上它和卷积神经网络是一样,都是为了解决某类问题,而在多层感知器的基础上添加了一些结构实现更多的功能,现在来详细看一下单向RNN的结构:
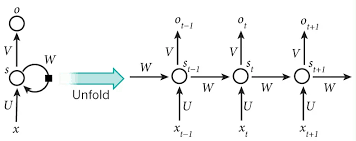
上图左方是循环神经网络的结构,右方则是根据时序数据而展开的结构,可以看出,上一个时刻的隐层的输出,既输出到输出层,也输出到下一个时刻的隐层,这样对一个时刻的隐层来说,它就同时分析了历史数据以及当前数据,使得RNN在某一时刻的输出不仅与该时刻的输入有关,还与该时刻之前所有时刻的输入有关,达到了记忆的目的。
从公式的角度,也可以这样看,对某一个时刻,有:
进一步展开,我们就能看到当前输出与历史输入的关系:
这样一直展开,我们就能看出历史所有输出对于当前输出都有影响。同时注意一下,在f中包含了f自身,也就是这是一个递归,所以RNN也叫递归神经网络。
明白了循环神经网络的基本结构之后,我们继续分析一下它的细节,第一是模型的输入,我们输入的是单词,一般采取独热矢量,根据单词在语料库中的位置进行输入(比如"我"排在语料库的第二位,那么它的矢量就表示为[0,1,0...],所以,这也意味着模型的输出是语料库中的单词,而不会模型自己制造出新的词,比如现在我们有一个大小10000的语料库,那么就意味着输入层有10000个神经元,输出层有10000个神经元。
第二个是关于模型的输出,一般来说,我们为了让模型输出是一个概率的形式(也就是说输出显示为语料库各个词的概率),我们会对输出做归一化处理,这种处理主要通过使用softmax函数作为输出层神经元激活函数来解决:
第三是模型的训练过程,完整输入一个句子为一个训练样本,而不是输入一个单词,这就意味着一次训练中会包含了多个输入,多个输出,而各个参数在这个过程中是不变的,在计算训练误差时,也是计算一次训练各个时刻的训练误差之和。我们进行的是有监督学习,所以每一个单词的输入都会有一个理想的输出的,比如用之前的例子,一开始先输入一个开始符,理想输出是"我",接下来输入一个"我",那么它的理想输出就是"今天",下一个输入是"上班",它的理想输出就是"迟到了",直到最后输入一个结束符,结束一个训练样本的训练。
上述的训练过程,和用智能拼音打字是相似的,一般来说我们打了几个字智能拼音就会预测接下来我们可能希望打的词,随着你使用智能拼音的时间越多,它的预测会越来越符合你的习惯,其实这就是一个训练的过程,同样,循环神经网络也是通过不断的训练,得到一个模型,它通过训练数据能够"记住"语料库中的词之间的搭配,以及句子的表达,归根到底就是通过大量数据获得一个概率模型,而不是真的达到一种智能,真的掌握了一门语言。
再次回到我们的模型,第四个需要关注的是模型的损失函数,因为我们的输出层使用了softmax函数作为激活函数,相应的一般会使用交叉熵误差函数作为模型的损失函数:
这是一个十分经典的损失函数,首先要明确式子中期望输出和实际输出的乘积是对应元素相乘再求和,比如:
可以看出,这样相乘实际上计算期望输出对应的概率的对数,比如说期望输出是"我",而模型计算得到的输出中"我"的概率是0.3,训练误差就是ln(0.3),所以它的概率越接近1训练误差就会越接近0。
关于模型的学习算法,会在BPTT中继续详细描述。
最后,再注意一下,上图是循环神经网络的展开图,只是同一个模型不同时刻的状态,所以w只有一个,不会出现不同时刻有不同的参数。另一方面,这种模型在不同时刻共用同一个参数的现象,称为共享参数。
通过上面的介绍,我们了解了循环神经网络的基本结构、它的输入输出、损失函数以及学习算法,但上面提到的模型是最基础的单向循环神经网络,为了解答另一类问题,我们还会有双向循环神经网络。
考虑这样一类问题,"我上班__,老板批评了我",这个例子和之前差不多,但是我们要推断的是句子中间的内容,这种情况需要根据句子前后的内容去理解,才能猜出答案,为了解决这一类的问题,就提出了双向循环神经网络:
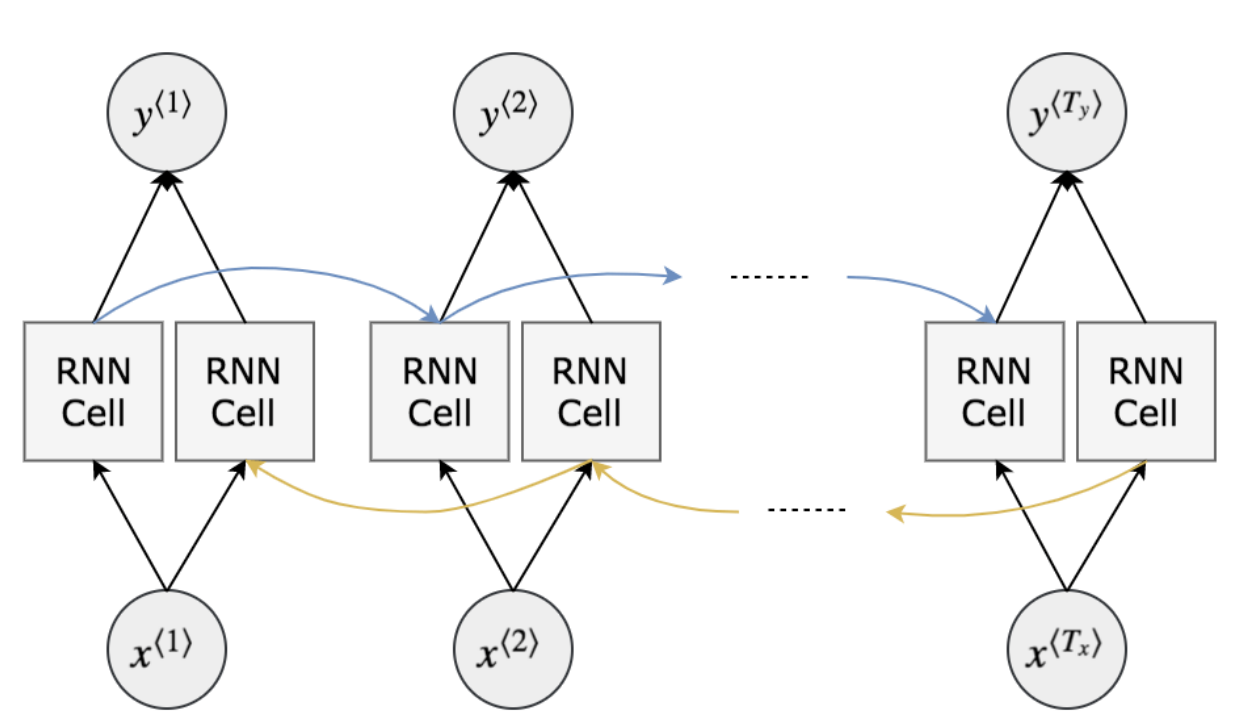
双向循环神经网络的训练过程,首先是通过前向神经元进行前向计算,就是正常的单向循环神经网络,之后,模型会通过反向神经元进行一次反向计算,两次计算的输出会作为输出层神经元的输入,再合并成每个时刻的输出。所以双向RNN和单向RNN的改进就是在隐层中加入多一个反向神经元,每一时刻的输出由前向计算和反向计算的输出决定。
从另一个角度也可以说双向循环神经网络就是把时序数据按照反序输入训练多一遍,达到让模型能够充分从句子的整体内容进行推导。