感知器
在正式介绍神经网络之前,首先来了解一下神经网络的前身,MCP模型(McCulloch-Pitts模型),简单来说他就是一个神经元的建模。
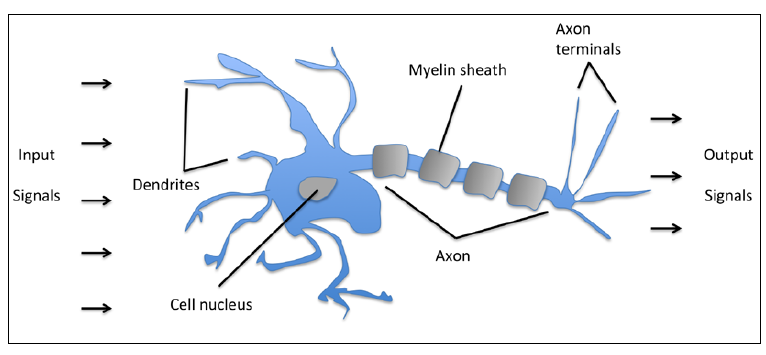
上图是生物意义上的神经元,也是我们要建模去模拟的神经元,根据生物的定义,我们建立的MCP模型主要简化成:接受多个输入,得到两种输出(1或者0),表示神经元的激活和抑制状态。用更数学的语言表达,就是:
f是激活函数,这里采用单位阶跃函数(也可以用分段线性函数、sigmoid函数等等),简单来说就是input满足一定条件输出就会为1,否则为0。以上就是基本型MCP模型,重复一遍整个模型的工作过程:当前神经元将同一个神经网络的若干个其他神经元的输出作为输入,然后对这些输入进行加权求和,如果结果小于阈值,则当前神经元的状态为抑制,输出为0,否则状态为兴奋,输出为1。
如果对基本型MCP模型进行适当的修改,比如把输出改为任意实数等等,就能得到增强型MCP模型,简单来说就是更一般的模型。
介绍完MCP模型,就可以进一步介绍感知器(perceptron)。感知器就是单个MCP模型,也可以说是只包含一个神经元的神经网络,更多应用于二分类问题。
感知器的具体实现过程如下:首先初始化权值向量,对每个向量赋初始值,然后把轮流每一个训练数据代进感知器模型得到输出,如果分类正确就训练下一个数据,分类出错的时候就对权值向量进行更新:
这里注重讲解一下这个参数(权值向量)的迭代更新原理。因为我们模型的输出只有0和1,如果模型分类错误就是说把1分类为0或者相反,假如说模型现在把0分类为1,那么为了修改模型,我们其实就是希望减少wx(输入与权值向量的向量积),使他小于阈值,就能被正确分类了,可是因为x是固定的,所以其实我们能减小的只有w,看回我们的迭代公式,Y=0(数据的真实标签),y=1(模型的预测标签),如果我们按照迭代公式求得新的w再计算wx,有:
可以看到,因为x是平方,所以新的wx一定比原来更小,符合我们的预期,至于小多少就由学习率来决定。同样的,如果我们分析另一种分类错误的情况也能得到同样的结果。
接下来我打算讨论一下它和逻辑回归的关系,因为这两种都是分类算法,算法上具有不少接近的地方,比如两者都是接受输入,把输入乘上权重,再代进一个函数里,从而决定所属分类。主要的区别是他们代进的函数不同,对逻辑回归来说代进的函数是logistic函数(sigmoid函数),输出是0到1之间的实数,然后再根据我们规定的阈值去进行分类,而使用单位跃阶函数的感知器,则是直接根据wx是大于0还是小于0得出输出为0或者1。所以,从另一个角度来说,逻辑回归就是用logistic函数作为激活函数的感知器。除此之外,我们也能看出对于分类问题,不像回归问题那样可以使用MSE作为比较通用的损失函数,根据具体的情况会有不同的选择。
介绍完单个感知器,就轮到多个感知器的组合了,首先是单层感知器,主要是因为感知器无法解决多分类问题而出现的,
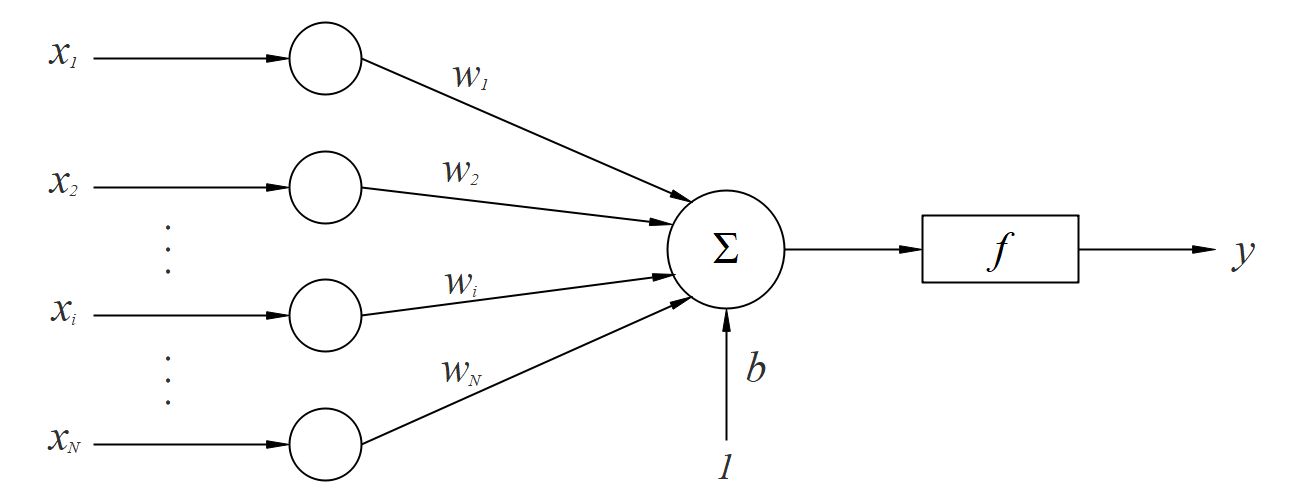
可以看到,单层感知器就是多个感知器并列在一起构成一层,重点为什么是多个感知器就能解决多分类问题,首先我们来回顾一下,单个感知器就能得到一个分类边界(超平面),从而实现二分类,如果两个感知器就能得到两个超平面,以此类推,m个感知器能获得最少不少于m+1个,最多不大于2^m个彼此不重叠的被超平面划分开的凸区域
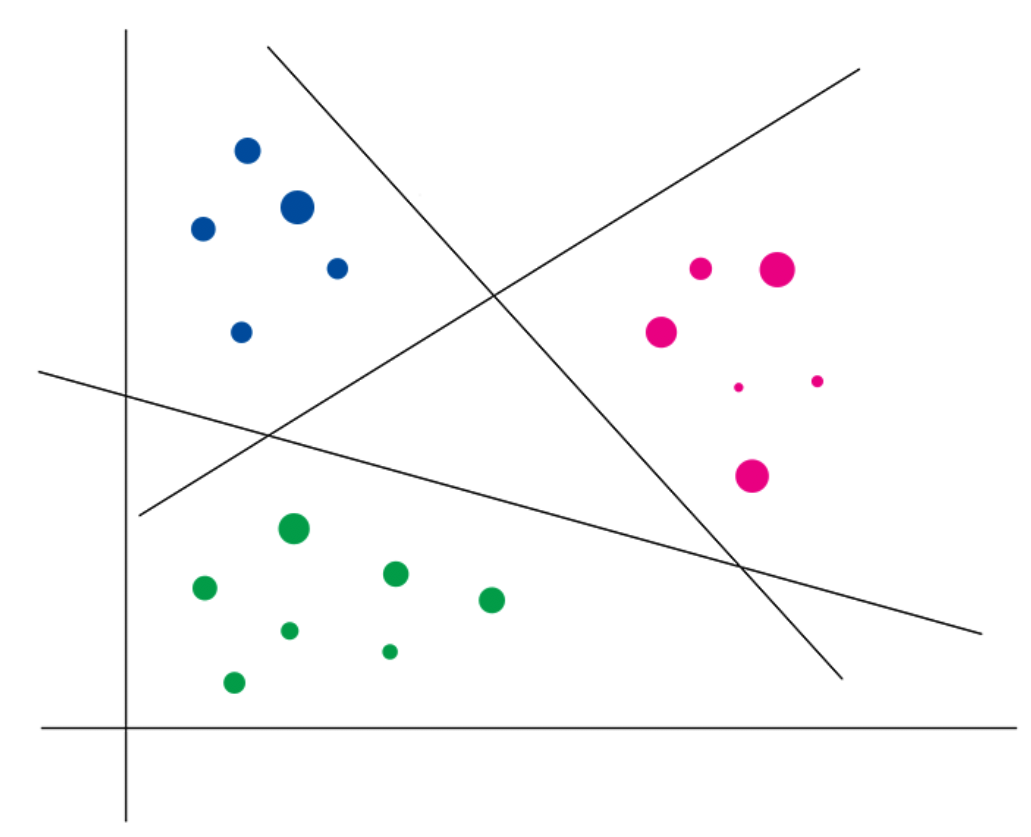
从上图就可以看出,利用三个感知器得到三条分类边界,划分出七个凸区域,实现了三分类。实际上,三个感知器分别是针对三个类别的,对每一个感知器,主要是划分是否属于某个类别,所以三分类就需要三个感知器,然后,划分出的七个区域,除了我们目标的三个分类区域外,还包括了不属于类别12的区域、不属于类别23的区域、不属于类别13的区域和不属于类别123的区域,因此一共有7个区域。用这个例子想说明的除了多个感知器能够解决多分类问题之外,还想说明其实我们划分了那么多个区域不等于就是每个区域都代表着一个分类。
最后还想说明一个问题,我们上面的例子都是(多)线性可分问题,如果两种类别的数据混杂在一起,即使是单层感知器也无法解决这种分类问题,但是现实中很多问题都涉及到非线性可分性,这就极大地限制了单层感知器的应用范围。