关于神经网络的个人见解
深度学习因为其强大的能力越来越被应用到不同的领域,深度学习,或者说深层神经网络,说到底还是神经网络,只是基于不同的问题可能会添加一些额外的结构,或者增加大量的隐含层以达到所谓的深度,但这些都只是后话,毕竟即使只是一个简单的线性回归模型我们同样可以做各式各样的改进,为什么就轮不到它那么火呢,这里我想谈一下我个人的一些看法。
首先从另一个角度来回顾一下最简单的全连接神经网络,这里我把它看成两个部分,一个是神经元,一个是网络结构。
所谓神经元,我觉得有点类似广义线性模型,以激活函数为sigmoid函数作为例子,本质上,如果一个神经元以sigmoid函数作为激活函数,那么它就是一个logistic回归模型了:把多个输入进行线性组合,然后通过sigmoid函数进行一个非线性变换:
为什么一定要非线性变换,如果不是非线性变换,那么到头来神经网络就只是一个复杂一点的线性模型了,所以这里的激活函数是神经网络的一大重点,虽然可能在不同情况下会采取不同的激活函数,但是非线性变换就是神经网络强大的原因之一。
第二点是网络结构,网络结构的核心就是把上一层的输出作为下一层的输入,比如上一层有三个输出:S1、S2、S3,那么对于下一层的某个神经元来说,就有:
这里还是以sigmoid函数作为激活函数,从这个函数的形式我们就能看出,上一层有三个输出,他们之间是一种线性组合,这个结论当然很明显,但是进一步推广,如果我们有一个可以表达整个神经网络的函数,那么我们就能通过线性组合这个特征去判断在同一层的神经元了。
上面的结论,主要是为了引出下面的另一个结论,首先我们来看一个复杂一点的函数:
S4至S9也分别有对应具体的函数,这里不再具体写出来,主要想说明的是,从函数的角度就能看出,对于不同层的神经元,我们可以通过它经历的非线性变换次数判断所在的层数,也可以说是sigmoid函数的内嵌次数去判断层数,为什么要强调内嵌,因为我想说明,整个神经网络函数虽然看起来很复杂,但本质上就是一个个sigmoid函数不断地嵌套生成的。
这种同一函数不断嵌套而复杂化的结构,是我本科毕业论文的课题,当时我研究的主要是多项式求根公式的嵌套结构以及与分形结构的关系,所以接下来我也想从分形的角度去分析神经网络结构。
根据上面的讨论,我们首先有一个结论,神经网络的结构,就是激活函数的不断内嵌的结构(暂假设整个神经网络都采取同一种激活函数),那么这种不断内嵌的结构有什么优点呢,从分形的角度来说,就是可以达到任意精度的复杂度。这里我先介绍一个知识点:有一种叫做希尔伯特曲线的分形曲线可以充满一个平面:
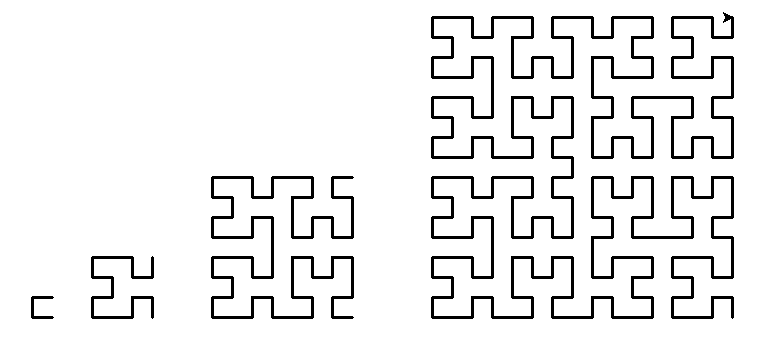
按照常识而言线是不可能充满整个平面的,但是因为分形可以达到任意的复杂度,使得分形曲线可以逼近充满整个平面。假如把平面看成一个解空间,我们的模型看成一条线,模型有很多,比如多项式回归,只要次数足够高,项数足够多,理论上它也可以拟合出很复杂的函数,也就是说它可以变成一条十分弯曲复杂的曲线,但是再弯曲的曲线也没法充满整个空间,只有神经网络这种具有自相似结构的解函数才能理论上充满整个解空间,所以,神经网络就成为了确确实实的万能函数生成器了。(或者说神经网络可以逼近任意的多项式回归模型,而多项式回归模型未必能逼近任意的神经网络)
根据上面的讨论,从另一个角度也可以看出,只有在我们要拟合的函数十分复杂的情况下神经网络才能有很好的效果(这里主要指耗时等各方面的权衡),不然拟合一个线性模型也用神经网络就是大炮打蚊子。
以上关于神经网络和分形结构的讨论仅仅是我个人的看法,因为还是初学者,可能对部分知识理论的理解有点偏差,仅供参考,欢迎讨论。如果在往后的日子有新的理解我也会及时更新。