BP神经网络
之前从单个感知器介绍到多层感知器,也介绍了反向传播算法,总的来说这些就是神经网络的基础内容,所以现在就来总结一下神经网络的知识点。
根据前面的介绍我们已经知道,神经网络就是由神经元构成的网络,神经元实际上和广义线性模型是非常相似的,举个例子,逻辑回归就是一种广义线性模型,它和线性回归的区别就在于对输入变量的加权组合加上了一个link function(sigmoid函数),使得输入变量的输出不再是线性的,而对于一个神经元,如果我们采用sigmoid函数作为激活函数,实质上他就是一个逻辑回归模型。
根据上面的结论,进一步的,可以说,对于使用sigmoid函数作为激活函数的神经网络,实质上就是由一个个逻辑回归模型通过串联和并联构成的一个网络结构。其中,串联的神经元之间相互没有影响,它们的输出会作为输入传递到下一层神经元,也就是和他们并联的神经元,这种结构,其实整个模型的输出表达式中也可以看出。
接下来我想重点分析,为什么神经网络可以以任意精度拟合任意复杂度的函数,或者说,为什么逻辑回归通过网络结构连接后,就能够实现非线性拟合。
回想一下,逻辑回归本身也只是一种线性回归模型,它的决策边界是线性的。这样说的原因是,重新考虑一下,如果我们选择阈值为0.5,有:
也就是说,到头来我们还是通过变量x和权重w的线性组合去判断分类结果,而sigmoid函数仅仅是改变了这个结果的输出,使它限制在[0,1]的范围内,避免了离群点(特征过于明显的数据)的影响。
因此,当我们的神经网络只有一层神经元,事实上是没有拟合非线性函数的,因为本质上他就是一堆线性模型的线性组合,到头来还是线性的。可是如果加多一层神经元又会有什么变化呢,这里看一下之前推导的两个神经元组成隐藏层、一个神经元构成输出层的神经网络的输出的表达式:
如果我们再按照之前的思路,把神经网络看成一个逻辑回归模型,假定阈值为0.5:
可以看到,这里权重与输入变量之间已经不再是单纯的线性关系了,因而得到的决策边界也不再是一条直线了。进一步的,基于sigmoid函数形状和以上的分析结果,我会分析为什么神经网络可以拟合任意函数。
我们可以简化一下,在上述的神经网络的输出层不添加激活函数,直接把上一层的输出的线性组合作为模型的输出,也就是:
从这里可以看出,模型的输出就变成sigmoid函数的线性组合。再回想一下,我们在进行密度估计的时候曾经用过直方图做近似:
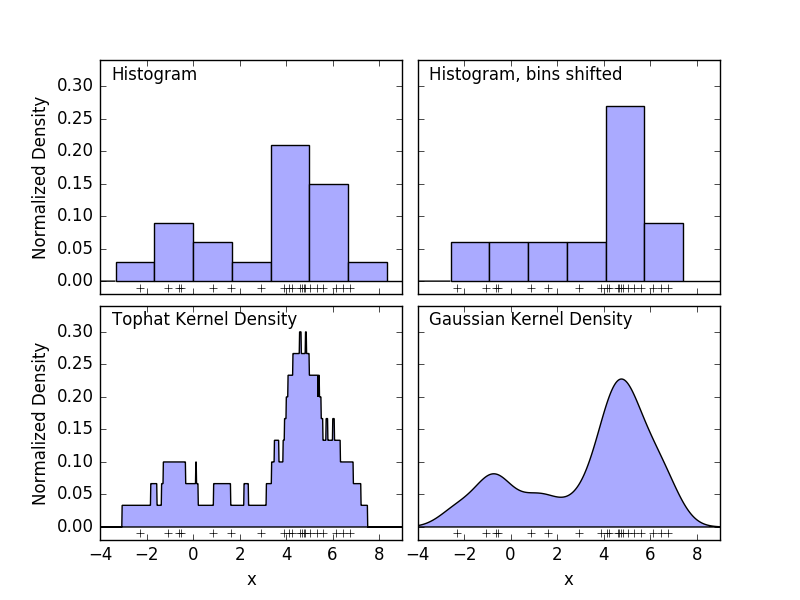
把sigmoid函数改成单位阶跃函数,把单位阶跃函数看成直方图的一个个矩阵,再把密度函数看成我们要拟合的任意复杂度的函数,就能得出结论,只要隐藏层的神经元足够多,那么用于拟合的矩阵就足够多,拟合的精度就足够细,到最后,即使我们只使用了一层隐藏层,也可以充分地拟合一个十分复杂的函数。
顺便再补充一下,关于神经网络中的sigmoid函数,它的形状和位置是十分灵活的:
可以看到,sigmoid函数中的z是x和w的线性组合,这就意味着,即使是对于只包含一个自变量x,sigmoid函数也可以在x轴上自由移动,形状随着权重w变得平缓或者陡峭,这种高度的灵活性就使得神经网络仅仅使用少数的隐藏层和神经元也可以高效地拟合复杂的函数。
通过以上的分析,基本上就可以明白神经网络比线性回归、逻辑回归更强大的原因,在于它通过线性模型、非线性函数的嵌套组合构成一个非线性的复杂网络结构,从而通过学习,调整参数,实现对任意复杂度的函数的拟合。归根到底,我们谈及人工智能,通过计算机去实现各式各样的任务,都是在拟合函数,再通过得到的函数进一步得出结果。