Network in Network
在介绍Network in Network之前,我们先再次重新思考一下,卷积神经网络的卷积运算的本质是什么。
按之前的定义,卷积运算可以理解成对一个二维的输入矩阵,对每一个局部位置与卷积核(一个矩阵)相乘并求和,计算得该局部位置的特征值
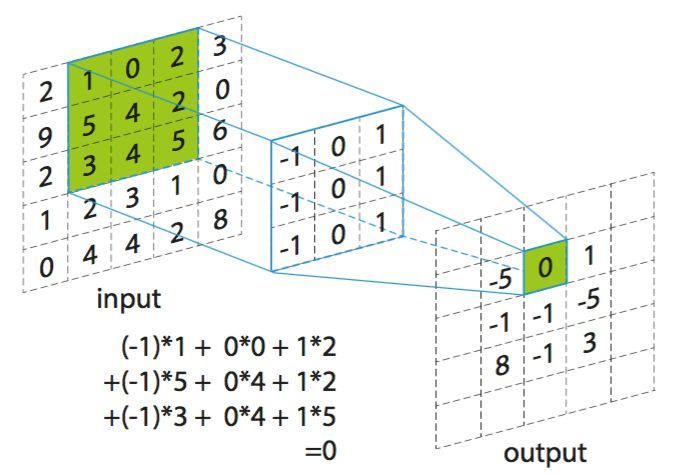
所以其实本质上,可以看成一个线性变换,输入一个m*n矩阵,输出单一的值:
可以看到,本质上来说卷积运算就是一个线性变换,所以这就是为什么一般的卷积神经网络,会在卷积运算之后加入一个非线性激活函数,不然搞再多卷积层,也只是在做一个复杂点的线性变换而已。同时激活函数也可以这样理解,比如我们用ReLU,如果特征值小于0,就直接取0,可以理解成特征不够明显就舍弃,这就避免了和特征无关的区域影响到模型的训练学习。
之前也提到,卷积层越深,就可以提取越复杂的特征,其实可以这样理解,以图像处理为例,比如模型现在要提取的特征是一个圆圈,模型怎么才能提取出来呢,首先我们要知道一个圆圈在图像中肯定是由多个像素点构成的,这就意味着对一个圆圈,它的每个局部其实可以看成一条直线(微分的思想),所以即使一个卷积核只能提取线性特征,模型也可以通过卷积核分析多个位置,利用这多个位置的特征构造出一个圆圈的特征,也就是之前提到的远距离特征提取,要实现这一步,就需要加深卷积层。
所以总的来说,CNN高层特征其实是通过底层特征,结合某种运算组合而成的,在图像处理中,如果对卷积核进行可视化,其实也可以看出底层特征都是十分简单的,层数越深,特征才会慢慢变得复杂:

通过上面的讨论,也可以进一步引出一个问题,如果我们要分析的特征高度非线性,那岂不是需要构建很多层卷积层才能提取出这个特征,而Network in Network这篇论文就提出了一个十分创新性的观点,为什么我们不改造一下卷积核,使得它能够提取非线性特征,这样不就可以用较少的卷积层,也能提取高度复杂的特征了。
Network in Network的第一个改进就是,把卷积层改为MLP卷积层,也就是用一个微型的多层网络作为一个卷积核。以前我们的卷积层可以写成以下形式:
现在改成MLP就变成:
Network in Network的第二个改进是,用全局均值池化,替换掉全连接层。一般来说,卷积神经网络最后会接一个全连接层,并用softmax实现分类,而这部分的参数占据了模型的大部分,大量的参数很容易导致模型过拟合。
首先,我们应该思考为什么普通的卷积神经网路最后需要一个全连接层,往往是因为之前的卷积层提取的特征还不够明显,所以需要全连接层进行处理,进一步通过特征分析出分类结果。而Network in Network为什么又不需要全连接层,而且效果也更好呢,可以认为是改进后的卷积层具备更强大的特征提取能力,经过卷积层处理后,已经不需要再利用全连接层去进一步分析,反而改进一下普通的池化层,直接输出分类结果已经足够了。
具体的过程是这样的,首先假设最后要进行二分类,在设计网络的时候,最后一层卷积层的特征图就会设定为两个,然后用全局均值池化,对每个特征图都输出一个结果,这样我们就可以得到两个输出,归一化后就可以作为二分类的结果。