卷积神经网络细节分析
之前曾经简单介绍过cnn的原理,但终究只是感性的理解,如果只是简单调用CNN肯定是足够了,但最近在研究CNN、RNN、Transformer在提取特征的优缺点时,深深感觉到如果不从公式层面推导一次各个模型,是无法深入理解它们的不同之处的。
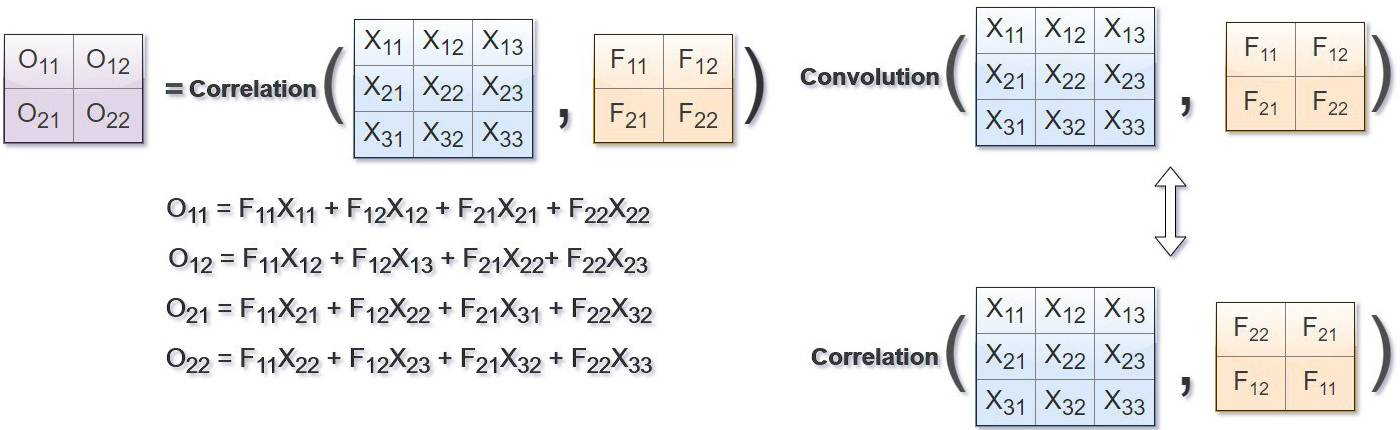
首先要分析的第一个问题是,卷积神经网络为什么不采用卷积运算而是用互相关运算。首先要知道,卷积层的作用是提取局部特征,卷积核需要遍历整幅图像才能获取局部信息,所以重点就在于卷积核的移动是怎么反映的,我们可以来看看卷积运算和相关运算的公式:
可以看到,不论是卷积还是相关运算都需要积分,求不同的x的值再加起来,不同的x就反映了需要计算不同"位置"的x的结果,这是卷积核的一种"移动"。
但是这个移动是一个方向上的,即使我们的输入是最简单的黑白图像,用二维矩阵表示,卷积核至少也需要在纵横两个方向移动:
公式中还有一个t,我个人认为另一个方向的移动就是通过公式中的t实现的,这个t可以理解成偏移量,或者一个新的方向的遍历,这个偏移量只存在于函数g。对g来说,就意味着计算结果时,既需要考虑不同位置的x,也需要考虑不同的偏移量t,如果把函数g理解成图像,那么公式就意味着函数f(卷积核)在函数g的x和t两个方向上遍历计算。
至于为什么卷积运算采用相关公式而不是卷积公式,首先可以看出相关运算和卷积运算的区别就在于那个正负号,可以理解成函数的"翻转",在其他领域这个翻转可能有其他目的,但是从卷积神经网络的分析过程来看,这个翻转没有特别的作用,所以在卷积神经网络中才一般使用相关运算。
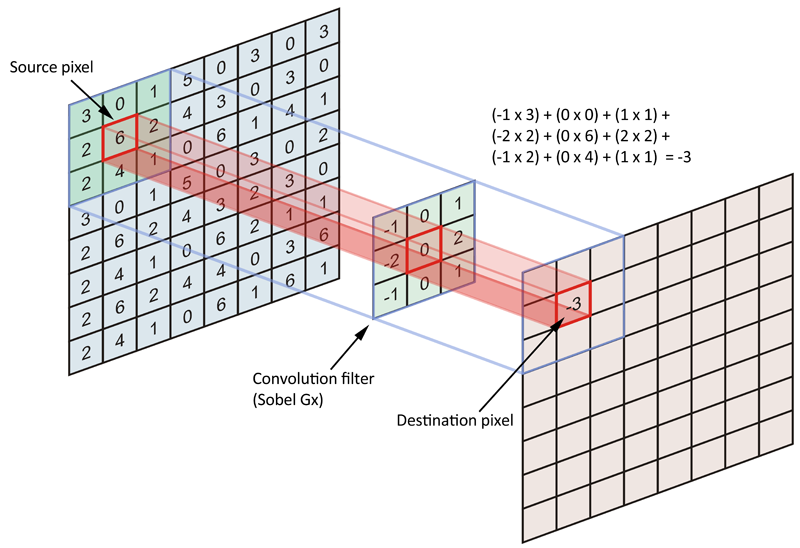
最后,再给出一个更容易理解的卷积运算公式,对于n*n的输入和m*m的卷积核,h是输出,可得到公式:
以上是关于相关运算和卷积神经网络中的卷积运算的关系的分析,接下来分析的就是如何用更加数学的形式去表示这个过程,或者说在实际编程中,我们是怎么实现卷积运算的。这里我举一个在书上看到的例子,假设我们有一个4*4的输入以及大小为3*3的卷积核,首先可以把输入展开为一维:
基于卷积核构建一个新的矩阵:
看着有点复杂,但尝试乘一下就知道为什么矩阵是这个形式了。
上面只是一个例子,主要想说明的是虽然我们在程序中可以通过循环来进行卷积运算,但效率十分低下,所以我们才需要矩阵,当然pytorch、tensorflow的卷积运算肯定还有更多的优化,这里只是想简单介绍一下卷积运算的一种实现方法。
最后再介绍一下CNN在NLP中的应用,也就是所谓的TextCNN:
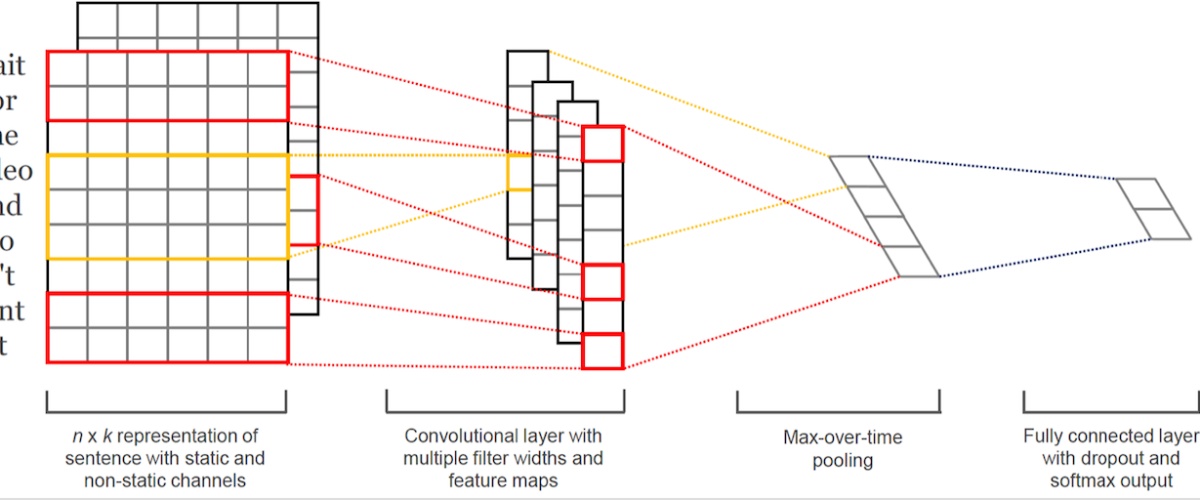
CNN能应用到自然语言领域的主要原因就是,经过embedding的一句话其实可以表示为一个二维矩阵,一维是词向量,一维是句子的各个词,然后我们就可以像处理图像那样处理文本了,只是有一点不同的是,图像处理中卷积核很多时候是一个正方形的矩阵,而textcnn的卷积核有一维的尺寸通常来说是等于词向量的维度的,比如现在有一句话包含十个词,词向量长度为300,那么我们可以采用3*300大小的卷积核,对句子进行卷积运算,这样卷积核每次滑动过的位置都是完整的单词,保证了单词作为语言中最小粒度的合理性。