BPTT与梯度消失（爆炸）

BPTT（back propagation through time)是针对RNN改进的学习算法，本质上还是梯度下降，主要是循环神经网络的结构导致求偏导的时候会比之前的情况更加复杂：
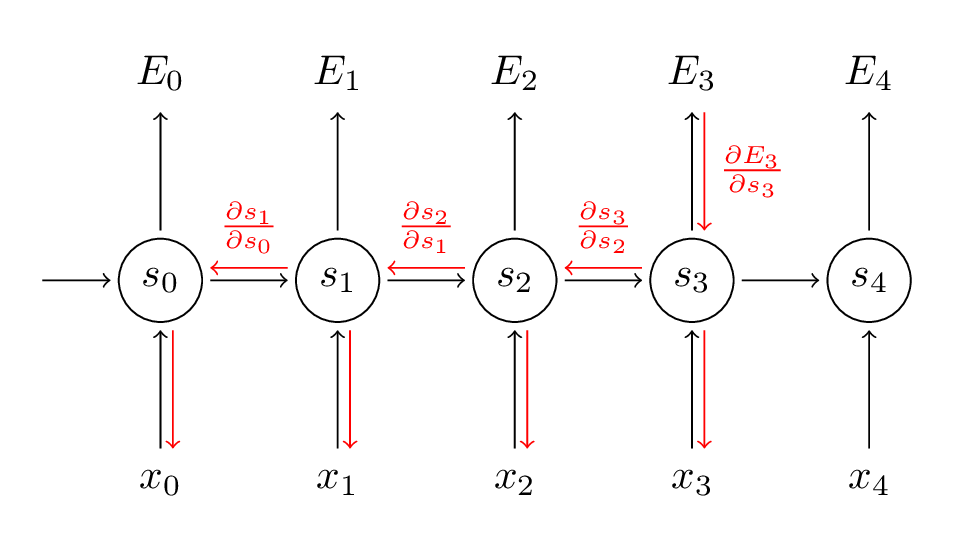
ポジショニングマップ
比如说我现在想求损失函数对w的偏导，根据链式法则：
$$\frac{\partial E_3}{\partial W} = \frac{\partial E_3}{\partial y_3} \frac{\partial y_3}{\partial s_3} \frac{\partial s_3}{\partial W}$$
可是问题是，s3依赖于s2：
$$s_3 = W*s_2 + U * X_3$$
也就是说，我们可以得到一个递归表达式：
$$s_t = W*s_{t-1} + U * X_t$$
注意，因为每个时刻的s都有一个同样的w，所以我们要对w求导的话，就需要在每个时刻都会w求导一次，再把各个时刻的结果加起来，以这个例子为例完整算一次：
$$ \frac{\partial s_3}{\partial W} = \frac{\partial W}{\partial W} * s_2 + w * \frac{\partial s_2}{\partial W}$$
$$ \frac{\partial s_3}{\partial W} = s_2 + w * \frac{\partial s_2}{\partial W}$$
同理得到：
$$ \frac{\partial s_2}{\partial W} = s_1 + w * \frac{\partial s_1}{\partial W}$$
$$ \frac{\partial s_1}{\partial W} = s_0 + w * \frac{\partial s_0}{\partial W}$$
因为s_0是常数，合并得到：
$$ \frac{\partial s_3}{\partial W} = s_2 + w^1 * s_1 + w^2 * s_0 $$
以上就是针对RNN的求导过程。

根据最后的结果可以看出，当我们的时间序列变长，最后一项的w的指数增加，这就导致了一个问题，当我们计算到某一时刻的w小于1，比如0.5，然后我们RNN考虑的时间长度为100，那么w的99次方就会变得非常小，由于计算机是有计算精度的，这么小的数就可能被计算机认为是0，这就是梯度消失的原因，同样，当w较大时，计算机也可能认为w为inf，造成梯度爆炸。