反向传播算法

之前提到神经网络在训练过程中需要根据预测输出和实际输出去调整权重和阈值，但是没有具体说明这个过程，在回归模型中我们往往会采用梯度下降法，这里介绍一种神经网络比较常用的方法，反向传播算法，本质上我觉得它还是梯度下降法。

首先我们采用实际输出矢量（actual output vector）和期望输出矢量（desired output vector）的欧式距离作为损失函数（一个简单例子）：
$$E_p = \frac{1}{M} \sum_{j=1}^M (y_{dpj} - y_{apj})^2$$
然后我们考虑一种最简单的情况，激活函数使用sigmoid函数，神经网络的隐藏层只有一层，包含两个神经元，最后就是一个包含一个神经元的输出层，再假设输入层有两个神经元（两个输入）：
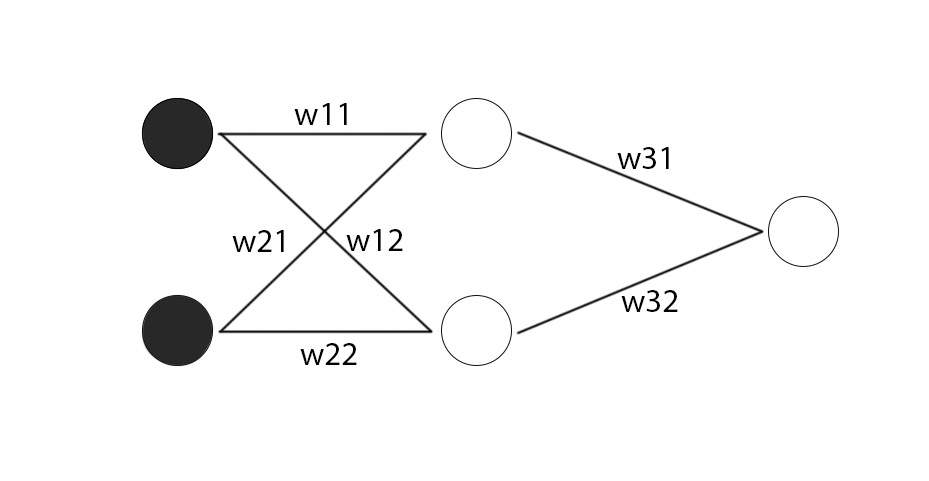
ポジショニングマップ
我们把两个隐藏层的神经元的表达式都写出来：
$$F_1(x_1, x_2) = \frac{1}{1+e^{w_{11} x_1 + w_{12} x_2 +\theta _1}}$$
$$F_2(x_1, x_2) = \frac{1}{1+e^{w_{21} x_1 + w_{22} x_2 +\theta _2}}$$
然后把两个神经元的输出作为输出层神经元的输入，得到：
$$y_{apj} = F_3(x_1, x_2) = \frac{1}{1+e^{w_{31} F_1(x_1, x_2) + w_{32} F_2(x_1, x_2) +\theta _3}}$$
最后我们得到了神经网络的输出的完整表达式，其中包含了输入x1、x2，以及各个权重w，事实上，这个比较复杂的表达式已经完整了表示了整个神经网络结构，如果我们把这个表达式代进损失函数里，就能得到一个包含了所有权重的损失函数的表达式，这时候，我们就可以利用梯度下降法的思想，通过损失函数对权重求偏导，得到权重的迭代公式：
$$w_{ij} ^{new} = w_{ij} ^{old} - \eta \frac{\partial E_p}{\partial w_{ij}}$$
只要我们通过这个表达式更新权重，那么损失函数就会不断降低了。