时间序列分析教程(一):基本性质
时间序列分析,其实就是和自然语言处理一样对序列数据进行分析,只是这里的序列数据是关于时间的序列,而自然语言处理是关于语言的序列。另一方面,时间序列也没有自然语言处理那样有很多分析目标,一般来说会有三种目标:描述历史数据的动态变化,分析数据变化的规律以及预测未来数据的变化趋势。
首先我会介绍一下时间序列的几个特征:平稳性、趋势性、季节性、周期性,一般来说,会希望时间序列具有其中一种或者几种特征的组合,这样的话就比较好分析,也有相应的模型,如果数据十分复杂,对数据进行转化等操作也不能显示出上述的特征,那么目前的时间序列模型就比较难分析了,或许就需要借助深度学习的模型了。
首先是最重要的平稳性(stationary),这也是最理想的性质,主要是假设随机变量的基本特征(统计性质)在未来的一个长时期内是保持不变,和过去一样的:
严格来说,如果对一个序列,对任意t都满足:
式子的意思就是即使有一个时间t的滑动,联合分布依然保持不变,以上称为强平稳。还有一种弱平稳:
我们看看强平稳和弱平稳,从公式来看,强平稳的条件更严格,但不能说满足强平稳就一定弱平稳。我个人觉得,强平稳就是一种很理想的情况,在这种情况下进行时间序列分析结果会很好,可是实际数据很难满足这种要求,所以才在强平稳的基础上提出条件稍微没那么严苛的弱平稳。但本质上来说,不论是强平稳还是弱平稳,都是在描述时间序列的统计性质关于时间平移的不变性。强平稳要求所有统计性质都是关于时间平移不变的,而弱平稳只要求期望和协方差是不变的。通过判断数据是否满足这些要求,就能分析出统计性质是否会在未来发生变化。
一般来说,强平稳太过理想,所以我们都是尝试把数据都转化为满足弱平稳条件再进行分析的。至于有哪些操作可以让原本不满足弱平稳条件的数据转化为满足弱平稳条件,后面会详细介绍。
关于平稳性,还可以引出两个函数,用于评价数据弱平稳的强度有多少,或者说有多接近强平稳,它们就是自相关函数(ACF)和偏自相关函数 (PACF),基于这两个函数,基于他们,我们甚至可以分析出一段序列中,哪一部分对预测未来最有用。
自相关函数用来度量时间序列中每隔 k 个时间单位(yt 和 yt–k)的观测值之间的相关性。统计中的相关性指的就是两个变量之间的相关程度,而这里则是指同一个序列中的两个不同的时间段的相关性,个人觉得和自注意力机制十分相似,对于一个弱平稳序列,有自相关函数:
是不是看着有点熟悉,因为本质上它就是皮尔逊相关系数:
因为自相关函数分析的是不同时间段的序列的相关性,不同时间段之间的滞后时间可能会对分析带来影响,偏自相关函数就是先剔除这些因素的干扰再分析相关性,这里先暂不细说。
如果时间序列满足平稳性就可以很好地利用现有的时间序列模型进行分析了,可是不满足就不能进行分析了吗,当然不是,如果说序列不满足平稳性,但是满足趋势性、季节性或者周期性,那么我们还是有模型进行分析的。
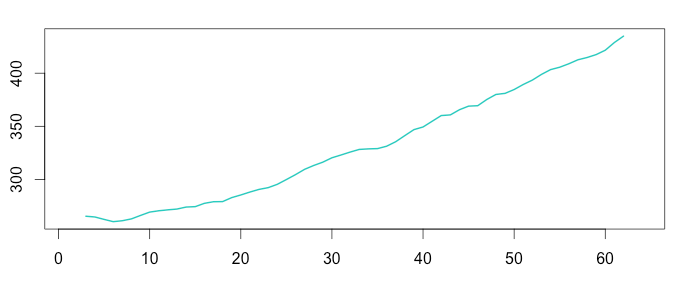
首先第一个是趋势性,可分为确定性趋势和随机性趋势。确定性趋势就是指序列的趋势可以用一条趋势线拟合,想办法剔除掉这种趋势后,序列就变成平稳序列了。另一种随机性趋势则是无法通过单一的趋势线分析的,在不同时间趋势是随机变化的。在后续的讨论中,我们主要是讨论确定性趋势,包括介绍如何剔除这种趋势进行建模分析。
第二种是季节性,像一年四季那样循环变化:
还有一种是周期性,和季节性一样也是循环的变化,但是变化的周期没有十分精确,是可以变化的,比如我们可以说一段序列每三个循环一次,它具有季节性,另外有一段序列,有时候三个月循环一次,有时候五个月循环一次,虽然看得出它有循环,但是循环周期不断变化,这就是周期性。为了简化问题,后续的讨论中主要分析季节性。
对现实数据来说,序列不是说有趋势性就没有季节性,而是往往平稳性、趋势性、季节性叠加在一起:
T_t表示确定性趋势变化,S_t表示确定性季节变化,X_t就是满足平稳性的时间序列。所以,我们才可以通过一些手段去掉趋势性和季节性,让序列变平稳再进行分析。