用逻辑回归(logistic regression)进行数据分析
网上用逻辑回归做分析的例子不少,但很多都是建了一个逻辑回归模型就结束了,这里将展示一个完整的分析过程,包括建模之后的分析和改进,我觉得这些过程有时候甚至比建一个模型重要,也要花费更多的时间。
首先我们来看一下问题,主要是分析一个人年薪能不能达到十万和什么因素有关(wage_status),响应变量是就是能不能达到年薪十万,解释变量就是年龄、婚姻状况等等:

第一步,我们可以探索一下数据,变量主要有数值型的变量和分类变量,先来看看数值变量,也就是年份和年龄,我们可以用回归样条画出两个变量和年薪十万的关系:
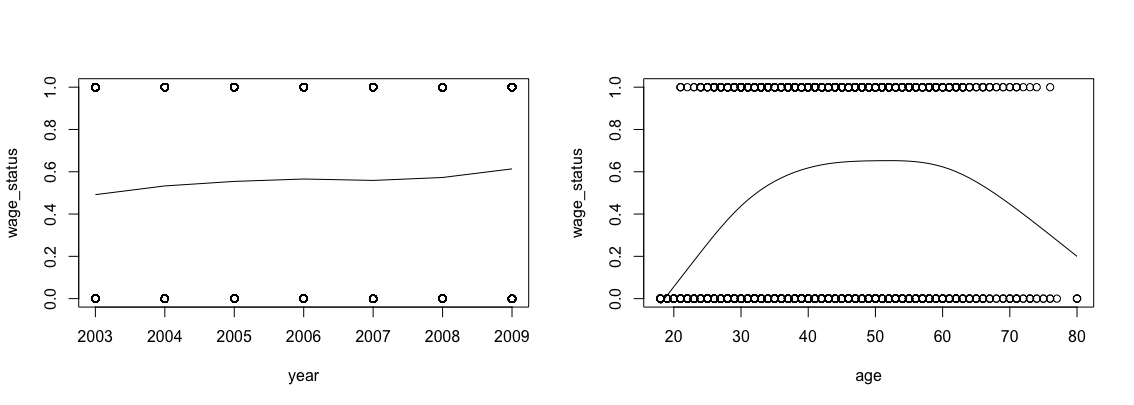
从左图可以看出,随着时间迁移,十万年薪的人确实慢慢增多了,而从年龄来说,四十到六十岁年薪十万的人是最多的,这个规律也很符合现实。同时也可以做一下wald检验,看看变量是否显著:

p足够小,说明可以用这两个变量进行建模。
关于类别变量,主要分析一下frequency table和卡方检验,这里就暂不细说了。而上述的分析,主要还是看一下变量对结果的影响是否显著,通过检验分析出都是显著的,所以我们可以用所有的变量进行建模。
当然,正如前面用GLM进行数据分析那样,可以用全部变量建模,不等于就要用全部变量,因为变量越多,越容易过拟合,所以这里还是通过AIC,在模型的准确度和过拟合的问题之间进行权衡,选择合适的变量进行建模。关于这部分的内容,感兴趣的也可以看回之前的文章,这里的重点还是放在模型的分析和改进,最后得到的结果是选择年龄、教育、婚姻状况、健康进行建模。
用逻辑回归建模,得到:
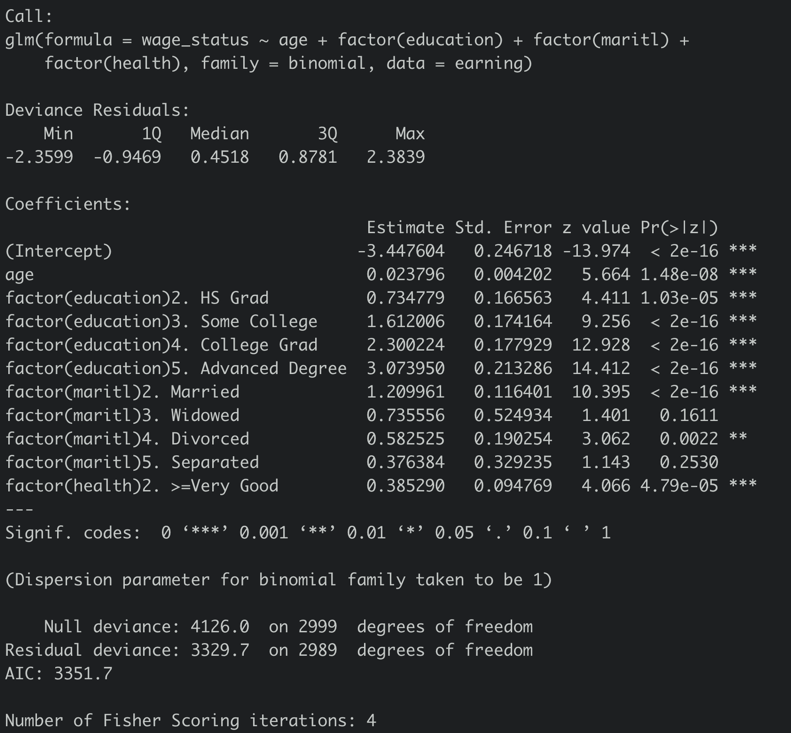
怎么看这个结果呢,首先我们可以写出模型的式子:
其中,xi1表示年纪,xi2表示教育是否为高中毕业,是就是1,否则0,其他类别变量也是像这样定义。
关于如何解释这些参数,首先要知道模型默认(reference)的对象就是一个教育水平低于高中毕业、从未结婚、健康为good的人,年龄作为数值型参数,每大一岁,那么年薪十万的概率就是增加exp(0.023796)-1=2.4%,如果他是高中毕业,那么年薪十万的概率就乘以exp(0.734779)=2.09,具体为什么是这样算,可以看看逻辑回归的公式推导一下。
基本上参数就是这样解释,可以看出,教育水平越高,年薪十万概率越大,结婚人群年薪十万的概率也最大,越健康年薪十万的概率也越大,这样看来这个结果还是挺合理的。
同时,我们也可以借助ROC曲线来分析模型的能力:
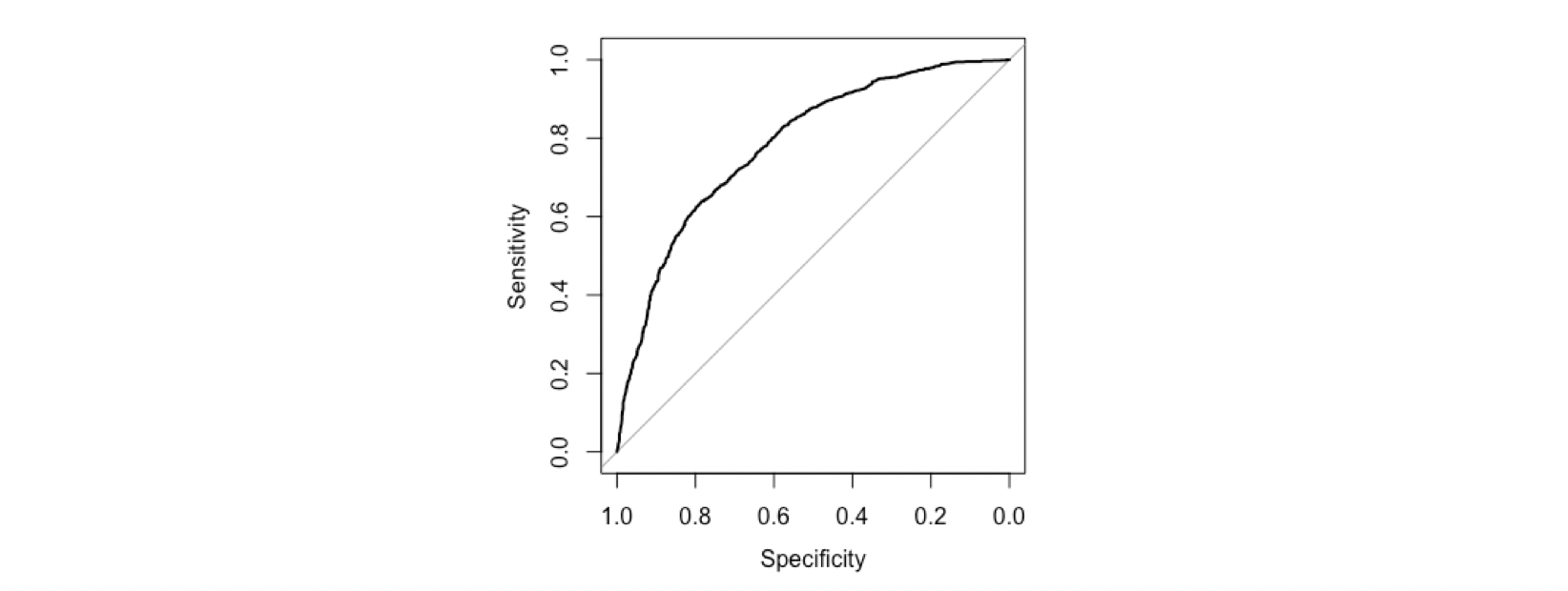
ROC曲线越往接近左上角越好,从这个角度来说模型还是不错的,起码比乱猜一个人有没有年薪十万好很多。
目前来说模型的结果还是可以接受的,但是还是有一个点可以改进的,那就是从一开始年龄和年薪十万的关系图像可以看出,其实年龄和年薪十万之间并不是简单的线性关系,注意一下,虽然逻辑回归用了link function,但本质上还是一个线性模型,因为因变量都是一次幂,而且他们之间服从线性关系,所以接下来,我们可以尝试一下在模型中引入关于年龄的非线性变换。
方法有很多,比如直接引入年龄的二次项、三次项,这里则直接使用GAM,用回归样条对年龄进行处理:
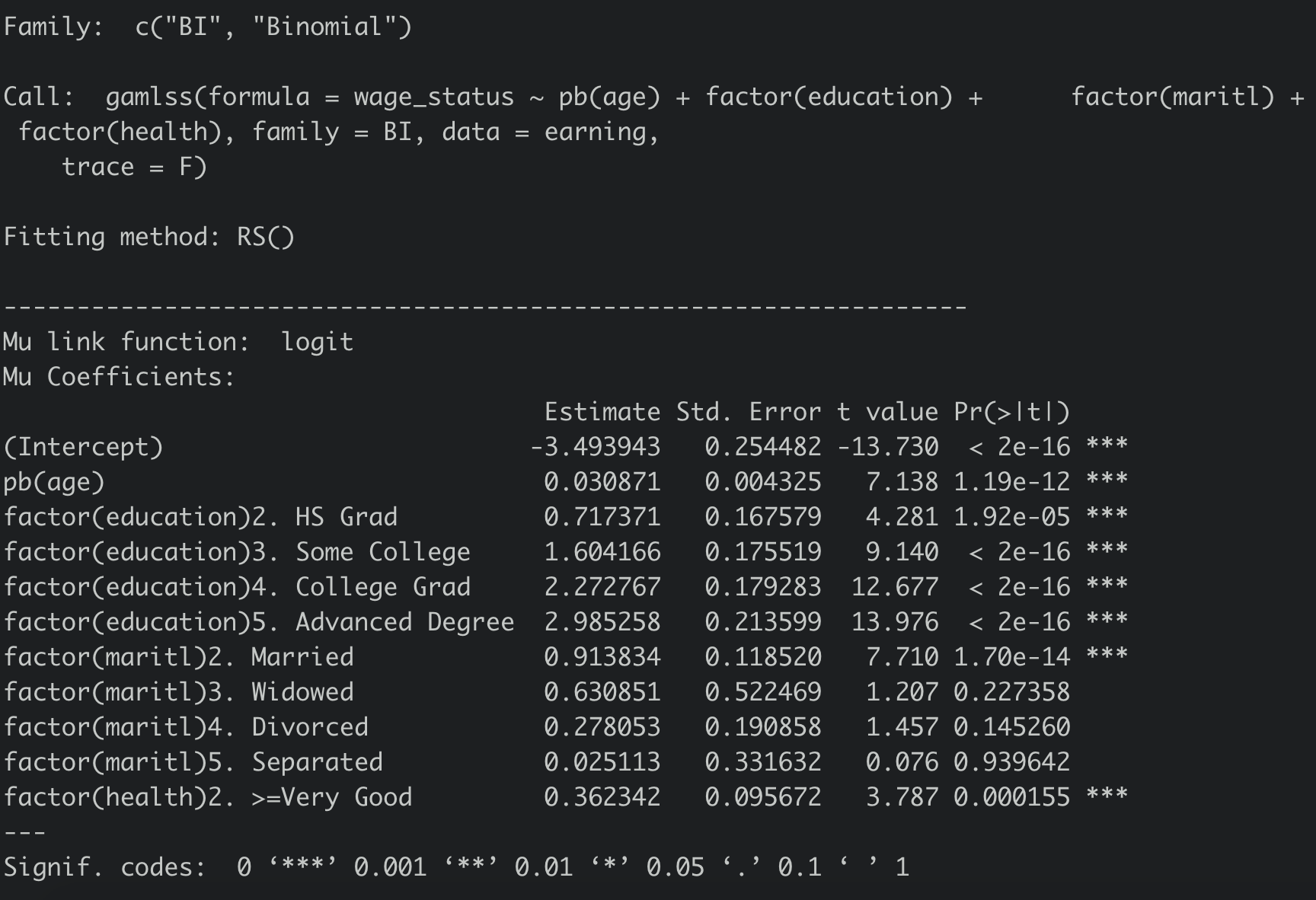
参数这时候已经有了变化,特别是年龄关于模型更显著了,当然,我们还是要通过AIC去比较这两个模型:

pb是R的回归样条的函数,所以从结果就可以看出,对年龄处理过之后,模型还是有一定提升的。