用GLM进行数据分析(下)
之前我们已经探讨了,在构建GLM模型之前,如何进行数据预处理,接下来就介绍一下正式的建模过程。
首先我们要做的是进一步具体地分析我们应该选择模型的变量。第一步是对一个个变量单独建模,观察他们的p值:
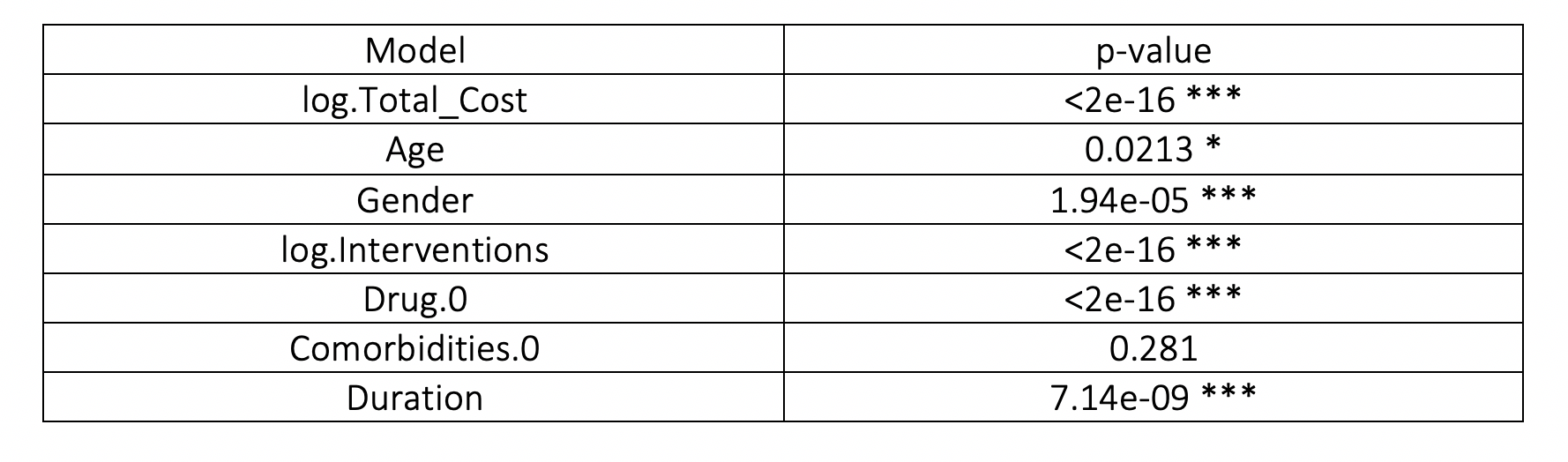
这个p值就是假设检验的p值,意思就是我们对模型的参数进行假设检验:
检验的就是变量的参数在等于0和不等于0的情况下(beta=0就意味着不考虑这个解释变量),模型是否具有显著的差异,在显著性水平为0.05的情况下,如果p值小于0.05,那么我们就有足够的理由去拒绝原假设,也就是认为模型考虑了这个变量会带来显著的变化,所以我们可以简单的认为,这个p值越小,变量对模型的结果影响越大。
所以根据上述的内容,我们就可以初步筛选出log.Total_Cost、Gender、log.Interventions、Drug.0和Duration作为模型的解释变量。
下一步就是进一步分析,如何用尽可能少的变量去得到尽可能好的效果,这样做的原因主要是因为,我们用更多的变量去建模肯定能得到更好的效果,但是有时候提升并不明显,而且也可能造成过大的方差,也就是过拟合,但是用的变量不够,有可能造成较大的偏差,也就是所谓的bias-variance trade-off,一般来说,我们会通过模型的AIC(赤池信息准则,Akaike Information Criterion)去判断模型的拟合优良性,AIC越低,模型就越好。
观察表格,可以看到log.Total_Cost的p值最小(其实log.Interventions、Drug.0也一样,选哪个没区别),我们就以这个变量开始构建模型,然后逐个加入第二个变量,再分析哪个模型的AIC最低,比如log.Total_Cost加Drug.0这个模型的AIC最低,就继续在这个基础上,加入第三个变量(Gender、log.Interventions或Duration),再分析哪个模型的AIC最小,当然,在这个过程中也要注意,如果不论加入哪一个新变量,AIC减小的幅度都比较小,我们就可以认为它们带来的帮助不大,就可以停止我们的分析过程了。这里我直接给出最后的结果:log.Total_Cost和Drug.0。
利用AIC,我们还可以分析用哪个link function的效果更好,因为对poisson分布来说,我们可以选择sqrt和identity两种link function(这里指R里面可选的参数),经过对比,最后发现sqrt的效果最好,这样,我们就可以定下模型的各个参数,构建出我们的GLM模型了:
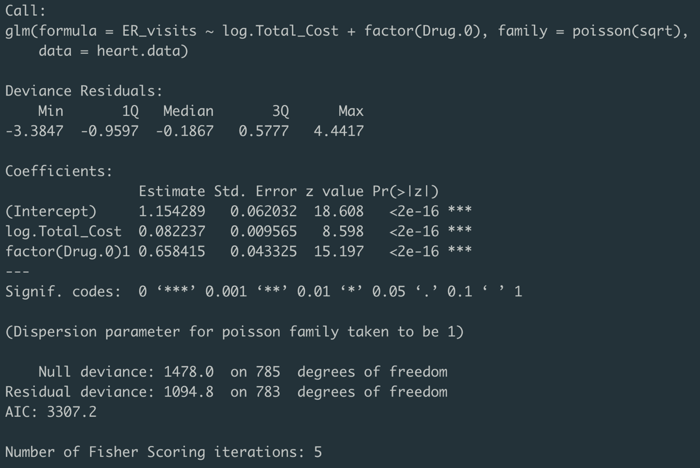
结束了吗,当然没有,因为这个模型的AIC实在是太大了,即使采取了最优的变量和link function,依然还是太大,所以接下来就需要进一步分析这个模型以及考虑如何改进了,一般来说我们会从三个角度去思考:第一,对于响应变量的分布的判断是否准确,第二,模型的解释变量和link function选择是否正确,第三,还有没有异常数据。
根据这个思路,我首先就尝试了其他分布,结合响应变量的分布曲线,以及它可以为0这一点,我尝试了高斯分布,然后重新进行了上述所有的选择解释变量的过程,再构建了一次模型:
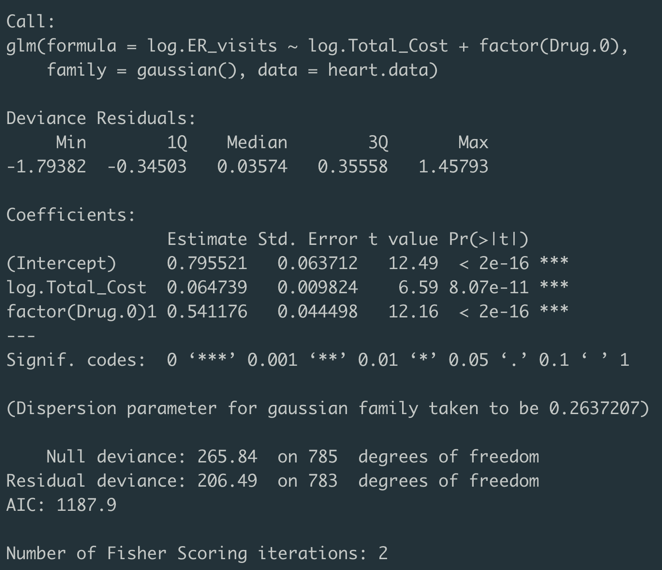
可以看到,这次模型的AIC就降低很多了,但是这个模型是不是一个好模型还不能下定论,还需要进一步结合一些指标进行分析,比如分析模型的leverage、deviance residuals、cook's distance等等,篇幅问题这里就不再一一细说了,一般来说,我会这样一整套流程走下去,从各个角度对模型进行评价,所以其实评价一个模型好不好,不仅仅是一两个数值可以说清楚的,包括我用了高斯分布之后模型的AIC下降了很多,也不能下定论说这个问题用高斯分布就一定比泊松分布好。
以上就展示了如何用广义线性模型分析一个实际问题,可以看到,不论是数据的预处理,还是建模之后的分析,GLM都有很高的要求,而且得到的模型还未必能很好地拟合数据,真的很麻烦,但是也不得不说,这整套分析过程是值得学习的,即使不用GLM,也可以用在其他模型上。